図形と計量

共通テストの図形と計量は正弦定理か余弦定理を使うつもりで待ち構えていれば解ける。
三角比は生徒から最も質問が多く、最も説明が難しい分野であるが、理解すると応用問題は大したことない。




三角比

直角三角形に置いて

sin,cosの値から角度を出す

単位円を書いてsin:y座標、cos:x座標だと考えているとわかりやすい。
cosA=12の場合
x=12の直線を単位円に書き込む


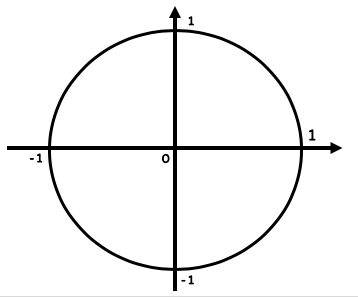
上記のような単位円を考える。

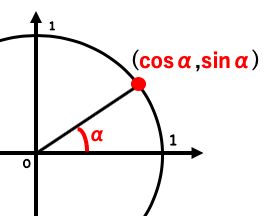
円周上のx座標：cosα,y座標：sinαである。

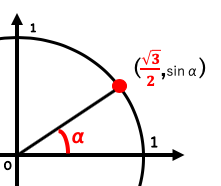
cos=√32の場合は直角三角形の底辺の長さが√32だとわかる。

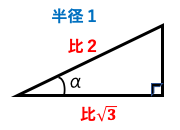
斜辺は円の半径であるため１である。

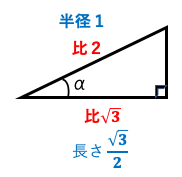
αが30度(16π)だとわかる。

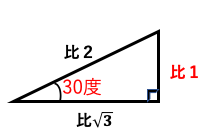
ただし0≤α<2πの場合は330度(116π)も含まれる。


正弦定理

asinA=bsinB=csinC=2R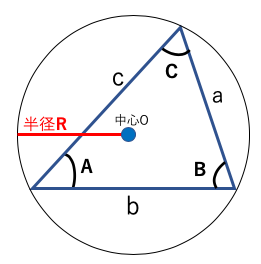

証明は余り理解する必要はない。

余弦定理

a2＝b2＋c2－2bccosA
角Aは辺aの対角である。

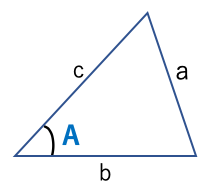
証明は余り理解する必要はない。

半角の公式語呂の歌↓


Short Notes

Homeに戻る