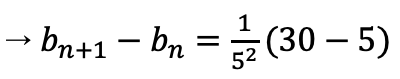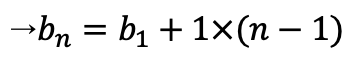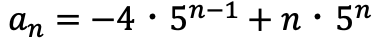数列
独学では習得がそれなりに程度難しい分野、公式の暗記量や想起の速さが必要。漸化式の特性方程式などのロジックを深く理解することよりも、まずは機械的に回答できることを優先したい。
漸化式のパターンは10程度あり、応用問題で図形が絡むとかなりきつい。
計算量が多く、数字が合わない場合が多い。
上位国立も含め、出題頻度が低い学部であれば捨てる戦略もアリ。
ただし基本的な10パターンぐらいはできないと全てのパターンに手が付けられないので定期試験で困る。
共通テストでも一応誘導はあるが漸化式を暗記していた方が予めシナリオを把握できるので早く回答できる。
ただし、2022年度本試験は問題文が難しかった。
できれば確率分布とベクトルを選択し、回答対象から外したい分野。
一日3時間の勉強で京大に合格した! 非常識な勉強法の秘術
等差数列
3,5,7,9,11,13,15初項3,交差2の等差数列。
のように初項a1,公差rの場合
an=a1+r(n-1)
等比数列
3,6,12,24,48,96初項3,公比2の等比数列
an=a1×rn-1
階差数列
項の差に規則性がある場合にΣを利用して一般項を求める。階差数列の具体例。
3,5,9,17,33,65,129
a1,bn=2nの階差数列になっている。
数列の和
Σk2は特に忘れがち↓
等比数列の和(初項a,公比r)
漸化式
特性方程式
an+1=2an+3,a1=10(an+1=α,an=αと無理矢理置き換える)
α=2α+3
→α=-3
(an+1-α=2(an-α)に無理矢理代入する[2はanの係数])
an+1+3=2(an+3)
an=(a1+3)2n+1-3
=13・2n-1-s
部分分数にして消去
f(n+1)-f(n)の形に持ち込む。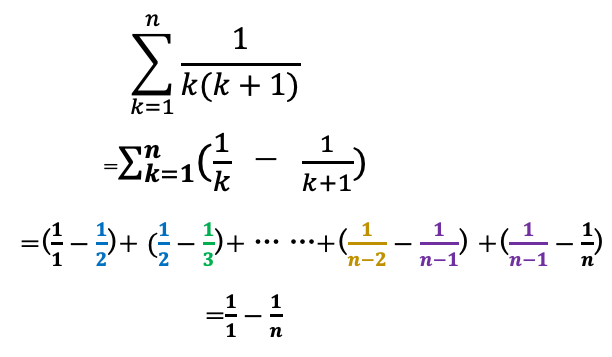
逆数を使う
-------------------例題--------------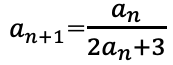
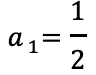
一般項anを求めよ。
----------------------------------------
an+1の逆数をとる。
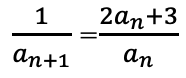
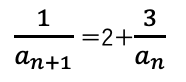
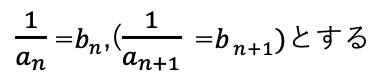
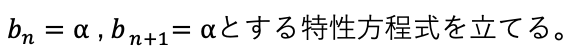
[αのみの特性方程式のパターン[an+1-α=係数3(an-α)]の等比数列に帰着する。]
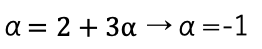
.png)
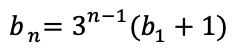
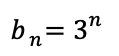
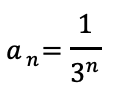
n-1項目を書き出して引く
---------------------例題---------------------an+1=3an-2n+5・・①
a1=4
-----------------------------------------
an+2=3an+1-2(n+1)+5・・②
②-①より
an+2-an+1=3(an+1-an)-2
bn=an+1-anと置き換えると
bn+1=3bn-2
α=3α-2
α=1
bn=3n-1(b1-1)
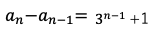
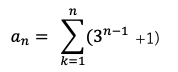
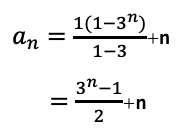
定数n+1で割る
----------------------------例題-----------------------an+1=2an+3n
a1=6
一般項anを求めよ。
---------------------------------------------------------
与式の両辺を3n+1で割る。
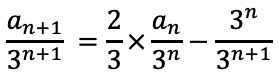
字数が多くなるので以下のように置き換える。
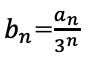
bn+1=bn+
[αのみの特性方程式のパターン[bn+1-α=係数(bn-α)]の等比数列に帰着する。]
α=α+
α=1
bn+1-1=(bn-1)
bn-1=()n-1(b1-1)
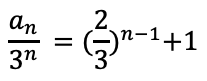
両辺に3nをかける。
an=3・2n-1+3n
logを使う
------------例題-----------------an+1=9an2
a1=9
一般項anを求めよ。
----------------------------------
bn=log3an
とする。
底は係数の9を消せるように3を設定する。(目的:log39=2)
bn+1=log39+2log3an
bn+1=2+2bn
α=2+2α
→α=-2
bn+2=2(bn+2)
bn=2n-1(b1+2)-2
bn=2n+1-2
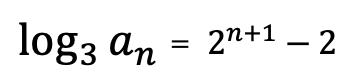
an=32n+1-2
和と差を取る
--------------------------例題----------------an+1=5an+bn・・①
bn+1=an+5bn・・②
a1=4,b1=2
------------------------------------------------
anとbnの係数が対称(5,1と1,5)の場合、二式の和と差を取る。
①+②より
an+1+bn+1=6(an+bn)・・③
an+bn=6n-1(a1+b1)・・③'
①-②より
an+-bn+1=4n-1(an-bn)・・④
→an-bn=4n-1(a1-b1)・・④'
③'+④'より
2an=6・6n-1+2・4n-1
→an=3・6n-1+4n-1
③'-④'より
2bn=6・6n-1-2・4n-1
→bn=3・6n-1-4n-1
隣接三項間
an+2,an+1,anの方程式の場合二次方程式の特性方程式で解く。例題:an+2-9an+1+14an=0
a1=2,a2=17
(与式のan+2をx2に、an+1をxに、anを1に無理矢理置き換えた特性方程式を作る。)
x2-9x+14=0
→(x-2)(x-7)=0
x=2,7
α=2,β=7とし
an+1-βan=α(an-βan-1)と
an+1-αan=β(an-αan-1)に代入する。
an+1-7an=2(an-7an-1)・・・①と
an+1-2an=7(an-2an-1)・・・②
①より
an+1-7an=2n-1(a2-7a1)・・・①'
②より
an+1-2an=7n-1(a2-2a1)・・・②'
②'-①'より
5an=7n-1(a2-2a1)-2n-1(a2-7a1)
→5an=13・7n-1-3・2n-1
→an=(13・7n-1-3・2n-1)
隣接三項間(重解)
例題:an+2-10an+1+25an=0(与式のan+2をx2に、an+1をxに、anを1に無理矢理置き換えた特性方程式を作る。)
x2-10x+25=0
(x-5)2=0
x=5
α=5とし
an+1-αan=α(an-αan-1に に代入する。
an+1-5an=5(an-5an-1)・・・③
③より
an+1-5an=2n-1(a2-5a1)・・・③'
ここで両辺を公比n+1(例題では5n+1)で割る。