円とおうぎ形
おうぎ形の面積と孤の長さ
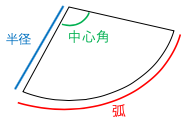
(おうぎ形の孤の長さ)=半径×2×円周率×
(おうぎ形の面積1)=半径×半径×円周率×
応用編：
(おうぎ形の面積2)=半径×弧の長さ×
(おうぎ形の面積2)の証明
(おうぎ形の面積1)=半径×半径×円周率×
=半径××(2×半径×円周率×)
=半径××(おうぎ形の孤の長さ)
=(おうぎ形の面積2)
(おうぎ形の周の長さを求める問題で２辺を足し損ねるミスが多い)
例題１：一辺が8cmの正方形の中の紫の斜線部分の面積を求めよ。
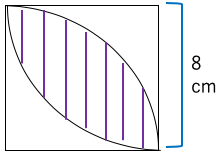
１解答：斜線部分を半分に分けて考える。
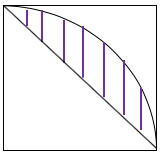
９０度のおうぎ形から直角三角形を引く。
8×8×3.14×-8×8×
=32×3.14-32
=32×(3.14-1)
=32×2.14
=68.48(cm2)
２倍すると求める面積になる。
136.96(cm2)
例題１：一辺が20cmの正方形の中に半径10cmの円を書いた図形である。
緑の緑線部の面積を求めよ。
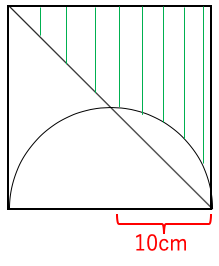
リンク
解答：
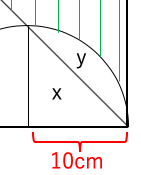
まず、yの面積を出すためにx+yのおうぎ形の面積からxの直角三角形の面積を引く
10×10×3.14×-10×10×
=78.5-50
=28.5
求める緑線部の面積は
10×10×-28.5
=21.5cm2
Short Notes
Homeに戻る