Short Notes

国立高等専門学校過去問

以下のページに過去問が載っている。
高専入試過去問リンク
本ぺージでは令和４年と令和３年度の過去問(数学)の解説を記載している。

令和４年度過去問

[1](1)
5.2²-4.8²
=(5.2+4.8)(5.2-4.8)
=10×0.4
=4

(2)
5x+6y=-2•••①
-4x+3y=25•••②

①-②×2より
5x+6y=-2•••①
-) -8x+6y=50•••②
--------------------
13x=-52
x=-4(ア)
①にx=-4に代入すると
-20+6y=-2
y=3(イ)

(3)(表が一回も出ない確率を計算し、全体の確率1から引くことを考える。)
表が一回も出ない確率は(

\frac{1}{2}

)⁴
=

\frac{1}{16}

表が少なくとも一枚出る確率は1-

\frac{1}{16}

\frac{15}{16}

(4)点数を小さい順に並べ替えると
2,2,2,2,2,4,4,7,7,10
中央値は5番目と６番目の2と4の平均の３
第３四分位数は８番目の７

(5)

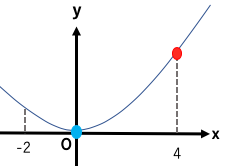
y=0のとき最小値0
y=4のとき最大値4

(6)

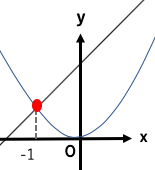
y=ax²
y=

\frac{4}{3}

x+2
二式を連立すると交点のx座標(x=-1)が出る式ができる。
ax²=

\frac{4}{3}

x+2

つまりこの式にx=-1を代入できる。
a=-

\frac{4}{3}

+2
a=

\frac{2}{3} (7)
                              内角を出していけば内角の和であるx度は分かる。

内角の和の公式[180度×(頂点の数-2)]の記憶が曖昧な場合は、点線で三角形を作り三角形の数に１８０度をかけたら内角の和が出る。 180度×4=720度 x=720度-(20度＋275度+7５度+280度+20度) x＝50度 (8)

(円錐の表面積)=(円周率)×(半径)×(母線+半径)を覚えてない場合。扇型の中心角を求めるのが王道。そのために扇型の弧を求める。弧の長さは円の円周と等しいので円周は4πであり、扇型の展開図の円周は6πである。角度は360度×

\frac{4π}{6π}

=240度
(扇型の面積)=3×3×π×

\frac{240}{360}

=6π(cm²)

(円の面積)=2×2×π
=4π²(cm²)

(円錐の表面積)=6π+4π
=10π(cm²)

大問[2]

(1)

CI＝xcm
CH=

\frac{x}{2}

三角形CIH=

\frac{x}{2}

×x÷2
=

\frac{1}{2}

x²

(2)

(

\frac{x}{2}

\frac{x-3}{2}

)×3÷2
[台形の面積=(上底＋下底)×高さ÷２を使用した。]

=

\frac{2}{3}

\frac{9}{4}

(3)
(長方形DEFG)=3×6÷2=9

\frac{2}{3}

\frac{9}{4}

=9

x=

\frac{15}{2}

を解くと

(4)
(

\frac{1}{2}

(1+h)²-

\frac{1}{2}

1²)÷(1+h-1)

=

\frac{h+2}{2}

------------------------------------------------------------------

大問[3]

(青字の)角DAB=105度、対角の和は１８０度より、
(赤字の)角DCB=75度
75度ー21度=x
角CPQとxは錯角で等しいため
角CPQ=54度
[求める角CPQと同じ角度がどこであるかを書き込んでおくのがポイント、
ただし(1)では同位角など使わない条件も多い]

(2)

円周角の定理で○と□が同じであり二角が等しいので
三角形ADPと三角形BCPは相似
AD:BC=3:4より
三角形ADPと三角形BCPの相似比は3:4
3.5×

\frac{3}{4}

=PC
PC=

\frac{3}{14}

(3)
BCが円の直径のため角CDB=90度
三角形CBDにおいて三平方の定理より
DB²+DC²=BC²
DB²+12²=20²
DB=16

PQ:BC=15:20
PQ:BC=3:4
三角形DPQと三角形DBCは相似のため
DP:DB=3:4
→DP:PB=3:1
DP=12,PB=4

円周角の定理より
角DAP=角CBP
角PDA=角PCB
二角が等しいので三角形PADと三角形PBCは相似

三角形CDPにおいて三平方の定理より
DC²+DP²=PC²
12²+12²=PC²
PC=12

\sqrt{2}

よって三角形PADと三角形PBCの相似比は1:

\sqrt{2}

x×

\sqrt{2}

=20より
x=AD=10

\sqrt{2}

[4]
(1)
ユニット１

(1,3)→(4,3)
ユニット２

(4,3)→(7,12)
ユニット３

(7,12)→(19,84)
[脳が疲れている場合は問題の意図を把握するのが難しいが、理解してしまえば代入するだけである]

(2)ユニット１においてx=1より
a+b=1
ユニット３において出力x＝-3より
a+b+ab+(a+b)×ab=-3
→1+ab+ab=-3
→2ab=-4
→ab=-2

[ユニット３の出力y=2を利用すると(a+b+ab)×(a+b)ab=2
→(1-2)×1×(-2)=2(が成立するが、確認以外では代入せずとも良い。)]

a+b=1,ab=-2を同時に満たすa,bのうちa < b を満たす数は
a=-1,b=2(オカキ)

(3)
ユニット１

ユニット２

ユニット３

(2+2b)(2+2b)=64
4(1+b)²=64
(1+b)²=16
b=3,-5

(4)
ユニット３に置いて(x,y)=(12,36)
[ユニット２において(x,y)=(6,9)]
回答欄にxの二乗が含まれているため
xの値を無理矢理二乗させて見ると 12²=144
これはy(36)の倍数になりそうなので割ってみる
144÷36=4となり
x^{2=4yが成り立つ

→y= $\frac{1}{4}$ x

[ユニット２でも同様の結果になるが、確認以外では計算せずとも良い]

リンク

------------------------------------------------------------------

令和３年度数学問題
[1]
(1)

-4× $\frac{5}{3}$ +6× $\frac{1}{9}$

=- $\frac{20}{3}$ + $\frac{2}{3}$

=- $\frac{18}{3}$

=6

(2)

2x²+8x-1=0
解の公式を使う。

2b'のパターンだと

(3)

y= $\frac{x}{a}$ ,y=-3x+1

$\frac{a}{4}$ - $\frac{a}{1}$ = $\frac{-11-(-2)}{3}$

$\frac{a-4a}{4-1}$ =-11+2

-3a=4(-9)

a=4×3

a=-12

(4)
y=ax-1にy=0を代入すると

1=ax
x= $\frac{1}{a}$

点C( $\frac{1}{a}$ ,0)だとわかる。

点B(( $\frac{3}{a}$ ,0))

点Aのx座標が $\frac{3}{a}$ なので

y=ax-1に代入するとy=2とわかる。

$\frac{18}{x}$ =ax-1

この等式のxは交点のx座標を表すのでx= $\frac{3}{a}$ を代入できる。

代入すると、a= $\frac{1}{3}$

(5)
当番以外の二人の選び方を考えた方が早い。

まずはAを含む組み合わせを考える。

(A,B),(A,C) ,(A,D), (A,E)の４通り。
次にAを含まずにBを含む組み合わせを考える。

(B,C)(B,D)(B,E)

A,Bを含まずにCを含む組み合わせを考える。

(C,D)(C,E)
A,B,Cを含まずにDを含む組み合わせは(D,E)のみ

合計10通り(スセ)。

別解：一人目の選び方は5通り二人目の選び方は４通り。
それぞれの組み合わせについて重複が必ず一組存在する[例：(A,B)と(B,A)]するから、

5×4÷2=10（通り）

(6)
最も多い度数が９のため最頻値は２(ソ)

冊数４の度数は６人のため

6÷36=0.1666...

四捨五入して0.17(タチ)

(7)

図中の1と2のプロセスにより角ABG＝２×○

対頂角により

角ABG=角EFH

CBH=80度(←180度-角ABC)

[別解：三角形ABEにおいて、角EAB+角AEB=角EBH]

角CBE=2×○-80度

錯角により角ICB=2×○-80度(=角CBE)

角ICJについて

2○-80度+2×＝１８０度
○＋×＝130度

x度＝○＋×により

x度=130度

(8)

球の体積 $\frac{4}{3}$ πr³(ゴロ？：身の上心配あーるさんじょう)
を使う。
36πh= $\frac{4}{3}$ π(5³+4³)

9h= $\frac{π}{3}$ (125+64)

9h= $\frac{π}{3}$ ×3×3×3×7

h=7

------------------------------------------------------------

[2]
囲われた４つの数(a,b,c,d)を強引にaだけで表すと以下のようになる

[↑カレンダーなどの問題で頻出の数値設定]

ad-bc=a(a+8)-(a+1)(a+7)

=a²+8a-(a²+8a+7)

=-7

(2)
n段目の一番左は１段目の１から７ずつ増加する。

n段目の一番左は1+7×(n-1)

=7n-6・・①

n段目の左から３番目(A)は7n-6に２を足した
A=7n-4(カキ)

４番目は B=7n-3(クケ)

A×B=1482

→(7n-4)(7n-3)=1482

→49n²-49n+12

→n²-n-30

→(n-6)(n+5)=0

nは正の数なのでn=6(コ)

①より、n段目の左から１番目は7n-6,一番右は7n

７項の和は{(7n-6)+7n}×7÷2[注：７項を逐一数えても良い]

=49n-21(=861)

n=18(サシ)

[3]
グラフが

(x,y)=(200,10500)と(100,3500)を通るので

10500=200a-b...①
3500=100a-b...②

①-②より

7000=100a

a=70[アイ]

a=20を②に代入

3500=7000-b

b=3500[ウエオカ]

(200,10500)と(100,3500)で引き算をすると

100秒で7000m走っていることがわかる。

7000÷100=70(m/秒)...③

単位の秒を分に直し、時間に直す。

70×60×60=252000(m/時間)

単位のmをkmに直す。

252000÷1000=252(km/時間)[キクケ]

x=70にy=0.35x²に代入する。

y=4900×0.35

y=1715(コサシス)

③より電車は秒速70mで電車が420mより。

電車の先頭がトンネルから出てから後部がトンネルから出るまでの時間は420÷70=6秒

したがって先頭部分がトンネルから出るのは216-6=210(秒)[セソタ]

70秒から100秒の間に走った距離を計算するためにx=100の時のyを出す。

y=0.35×100×100

=3500

3500-1715=1785(m)

100秒から216秒まで走った距離を計算する。③より

(210-100)×70=7700

7700+1785=9485(m)[チツテト]

---------------------------------------------------

[4]
(1)

ACDEは正方形だからAE=AC

三角形ABCは二等辺よりAC=AB

したがってAE=AB

つまり角AEB=x度(=角ABE:図中の赤実線部🟥)

二等辺三角形の垂線は角の二等分線でもあるので角CAH=y度(=角BAH)

したがって三角形ABEの内角において2x+2y+90度＝180度が成り立つ

x+y=45度[アイ]

[少し難]

(2),(3)

[(3)の誘導を見てから(2)を回答した方が楽に進められる。]

図中の①より①の角は外角のためx+y(=45度)

AHBは９０度のため

②EBC=45度

ABHは45度＋x度

三角形ABCは二等辺のため③角ACB＝４５＋x度

(3)の誘導により

三角形ABCと三角形DEFは合同

よって角DEF＝x度+45度

角DEA=90度、角BEA=x度より

x度＋(４５＋x)度=９０度

x=22.5度[ウエオ答]

角DEF=45＋x度より

角DEF=67.5度[カキク答]

三角形ABCと三角形DEFは合同であるので

EF=BC=4[ケ答]

(4)

三角形FGEと三角形FABが相似である。

(二角が等しいため)

相似比を考える。

正方形の一辺をxをおくと、

三角形ABCが二等辺三角形なのでAB=x

三角形AEGにおいて、AE:EG:GA= $\sqrt{2}$ :1:1

これより、EG＝ $\frac{x}{\sqrt{2}}$

三角形FGEと三角形FABの相似比は1: $\sqrt{2}$

相似比がわかったのでAFとFGの長さが図のようにわかる。

AF:FB=GF:FE

→AF×FE=FB×GF

→x²=16 $\sqrt{2}$ +32

(三角形AEFの面積)=AF×GE÷2

(三角形AEFの面積)=4[コ]

[(4)は相似に気づくのが難しく、整理も面倒なため、本番では序盤で回答するのは避けるべき問題]}

Short Notes

Homeに戻る