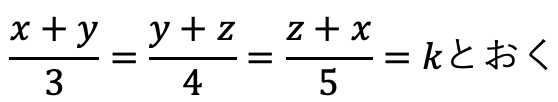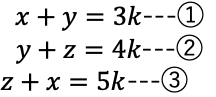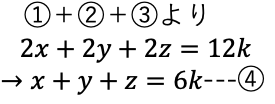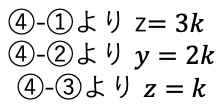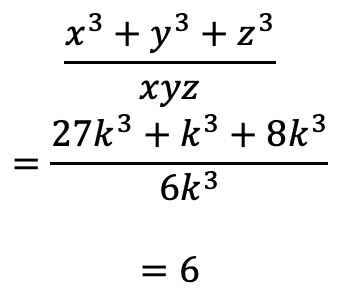いろいろな式
3次式の展開、因数分解
(a+b)(a2-ab+b2)=a3+b3(a-b)(a2+ab+b2)=a3-b3
(a+b)3=a3+3a2b+3ab2+b3
(a-b)3=a3-3a2b+3ab2-b3
剰余の定理
剰余の定理:整式P(x-α)を一次式で割った時のあまりはP(α)---------------------------------------------------
例題:2x3+3x2+4x+aがx+1で割り切れるとき、 aの値を求めよ。
---------------------------------------------------
剰余の定理より
P(-1)=0
→2×(-1)3+3×(-1)2-4×(-1)+a=0
→a=3
-----------------------------------------------------
因数定理
整式P(x)がx-αを因数に持つ↔P(α)=0剰余の定理の余りが0の時が因数定理である。
---------------------------------------------------
例題:x3-2x2+x-2=0を因数分解せよ。
---------------------------------------------------
与式に2を代入すると23-2×22+2-2=0
因数定理より
x3-2x2+x-2はx-2で割り切れる。
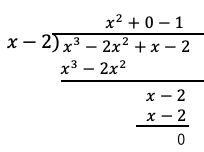
答:(x2+1)(x-2)=0
-----------------------------------------------------

二項定理
(a+b)n=nC0a n×b0+nC1 an-1×b1+...+nCn-1a1×bn-1+nCna0×bn(数学Aの確率や整数で使用する。)
相加平均、相乗平均
0<a,0<b,のとき≤, が成り立つ。比例式
例題: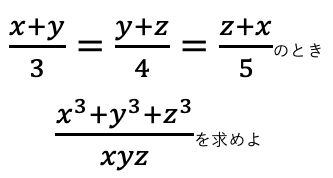

比例式をkとおくのがポイント↓