割合と比
割合、比は受験算数の要所だと言われる。ここをクリアできるかどうかが偏差値40台中堅中学に入学できるかのボーダーになりやすい。
----------------規則性(目次)-----------------
割合/比
組み合わせ/食塩水
----------------------------------
割合
割合=比べる量÷もとにする量比べる量=もとにする量×割合
もとにする量=比べる量÷割合
実質全て同じ式である。
かけ算の式:比べる量=もとにする量×割合だけ記憶して変形しても良い。
例題1:岡田選手の体重は100kgで五十幡選手の体重が岡田選手の体重ののとき
五十幡選手の体重は何kgか?
例題1解答:もとにする量は100kgで割合がなので、
100×=65(kg)
例題2:堂安選手の年収は7000万円,三苫選手の年収の
三苫選手の年収はいくらですか?
例題2解答
7000万円が三苫選手の年収のに相当するので、
三苫選手の年収は7000÷=17500(万円)

例題2別解
比べる量=もとにする量×割合に数字を入れて変形しても良い。
堂安=三苫×
両辺にをかける。
堂安×=三苫
7000×=三苫
三苫=17500(万円)
比
例題1:等積の長方形A,長方形Bがある。A,Bの横の長さの比が3:7の場合、A,Bの横の長さの比を求めよ。
らくらく文章術ドリル 作文教材 1括払い~24分割払い用
例題1解答:逆比なので7:3になる。
7:3になる理由。
A,Bの横の長さを7cm,3cmとし,
A,Bの面積を21cm2とする。
Aの横の長さは21÷7=3(cm)
Bの横の長さは21÷3=7(cm)
A,Bの長さの比は3:7
例題2:
姉と妹の年齢の比は9:7で妹の年齢は28才である。
姉の年齢は何歳か?
例題2解答:姉の年齢を△才とすると
9:7=△:28
外項の積=内項の積なので
9×28=△×7
9×28÷7=△×7÷7
△=36(才)
例題3:比を簡単にしなさい。
: :
例題3解答分母の最小公倍数の30をかけて整数にする。
15:70:12
例題4:山田、坂本、中田のスキャンダルが写真週刊誌に掲載された回数の比が
1:7:2であり3人が掲載された回数は合わせて20回である。
それぞれの掲載回数を求めなさい。
例題4解答:三人の掲載回数をそれぞれ①,⑦,②とおく,
掲載回数の和は①+⑦+②=➉
➉=20(回)より
①=2(回)
三人の掲載回数は①×1:①×7:①×2
山田2回,坂本14回,中田4回答え。
食塩水
食塩水は水と塩からできている。食塩水の重さ×濃度=食塩の重さ
食塩の重さ÷濃度=食塩水の重さ
方程式が使える生徒はいずれかの式を一つ記憶しておき、問題文の数値を当てはめれば十分である。
濃度(%)=×100
濃度について百分率と小数があり紛らわしいので例題を一つ挟んでおく。
例題1:百分率を小数に、小数を百分率に直せ。
(1)0.41
(2)75%
(3)1.3

例題1:解答
(1)小数を百分率に直す場合には百をかける。
0.41×100=41(%)
(2)百分率を小数に直す場合には百で割る。
75÷100=0.75
(3)例題1(1)と同様だが
1.3×100=130(%)
100をオーバーしても問題ない。
例題[2]
(1)30gの食塩を水120gに溶かすと濃度何%の食塩水になるか?
(1)解答
塩の量と水+塩の合計量がわかれば濃度は出せる。
水+塩=30+120
=0.2
問題では百分率(%)で答えないといけないので0.2×100=20(%)
例題[2](2)40gの水に塩を何%溶かすと20%の食塩水になりますか?
(2)解答
できた食塩水の20%が食塩に相当するため80%が水に相当する。
水40gが食塩水の80%に相当するため、食塩水の重さは
40÷0.8=50(g)
食塩の重さは50-40=10(g)
(2)別解[方程式用]
求める塩の重さをxgとする
=20(%)÷100
→=
100x=20(40+x)
100x=800+20x
80x=800
x=10(g)
例題1は公式を暗記していれば回答できる。
例題3:30%の食塩水100gに水を何g加えると,20%の食塩水になるか?
[水を加える前後で食塩の重さは変化しないため、
先に食塩の重さを計算する。]
100(g)×=30(g)
これが水を足した食塩水の20%に相当するため、
30÷0.2=150(g)ができた食塩水の重さ。
加えた水の量は
150-100=50(g)
[水を足すパターンでは食塩の重さが操作前後で変わらないことがポイント]
例題4:5%の食塩水が100gあります。
水を何g蒸発させると8%の食塩水になりますか?
例題4解答:蒸発の前後で食塩の量は変わらない。
食塩の重さは100×=5(g)
食塩5gが蒸発あとの食塩水の8%に当たるので。
5÷0.08=62.5(g)
したがって蒸発させた量は100-62.5=37.5(g)
[水を蒸発させるパターンでも食塩の重さが操作前後で変わらないことがポイント]
例題5:2つの食塩水を混ぜる。
100g5%の食塩水Aに特定の濃度の食塩水Bを混ぜると
150gで7%の食塩水ができました。
混ぜた食塩水の濃度は何%か?
<中学受験>子どもが自分から机に向かうようになる秘訣
例題5解答
塩の量を計算する。
食塩水A:100×0.05=5(g)
食塩水A+B:150(g)×0.07=10.5(g)
したがって食塩水Bに含まれる塩の量は10.5-5=5.5(g)
食塩水Bの重さは150-100=50(g)より
濃度は5.5÷50×100=11(%)答え
例題6:食塩水を加える。(偏差値50レベル)
濃度10%,100gの食塩水に濃度25%の食塩水を何gか混ぜて20%の食塩水を作成した。
加えた食塩水は何gか?
例題6解答:食塩の重さと合成後の食塩水の重さがわからないので、
例題5の解法では回答できない、比を使った面積図を使用する。
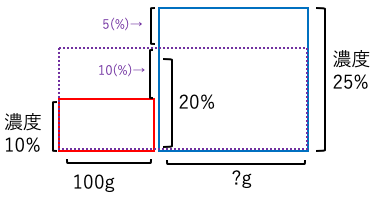
横軸が二つの食塩水のグラム数、縦軸が食塩水の濃度である。
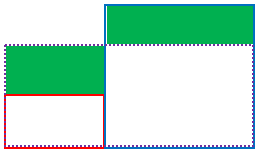
2つの緑の長方形の面積は等しい。
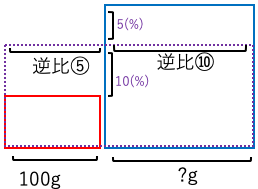
2長方形の縦の長さが5:10のため、
横の長さの比は逆比の10:5だとわかる。
100(g):?(g)=5:10
内項=外項より
100×10=?×5
1000=5×?
1000÷5=5×?÷5
?=200(g)答え
例題6別解:方程式を利用できる生徒にとっては簡単。
加えた食塩水をxgとする。
(100+x)×0.2=0.25x+10
20+0.2x=0.25x+10
10=0.05x
x=200(g)答え
----------------規則性(目次)-----------------
割合/比
組み合わせ/食塩水
----------------------------------
濃度10%,100gの食塩水に濃度25%の食塩水を何gか混ぜて20%の食塩水を作成した。
加えた食塩水は何gか?
例題6解答:食塩の重さと合成後の食塩水の重さがわからないので、
例題5の解法では回答できない、比を使った面積図を使用する。

横軸が二つの食塩水のグラム数、縦軸が食塩水の濃度である。

2つの緑の長方形の面積は等しい。

2長方形の縦の長さが5:10のため、
横の長さの比は逆比の10:5だとわかる。
100(g):?(g)=5:10
内項=外項より
100×10=?×5
1000=5×?
1000÷5=5×?÷5
?=200(g)答え
例題6別解:方程式を利用できる生徒にとっては簡単。
加えた食塩水をxgとする。
(100+x)×0.2=0.25x+10
20+0.2x=0.25x+10
10=0.05x
x=200(g)答え
----------------規則性(目次)-----------------
割合/比
組み合わせ/食塩水
----------------------------------
Short Notes
Homeに戻る