体積と表面積
底面積
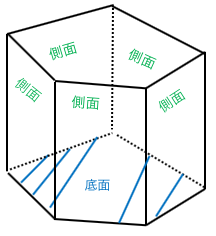
角柱と円柱の体積:底面積×高さ角柱円柱の側面積:底面の周りの長さ×高さ
角柱円柱の表面積:底面積×2+側面積

水量変化
容器に棒を立てる問題。(水の底面積=容器の底面積-棒の底面積)
例題:1つの直方体の水槽に3cmの水が入っている。
この水槽に図中の緑の棒を入れた時の水の高さは何cmか?
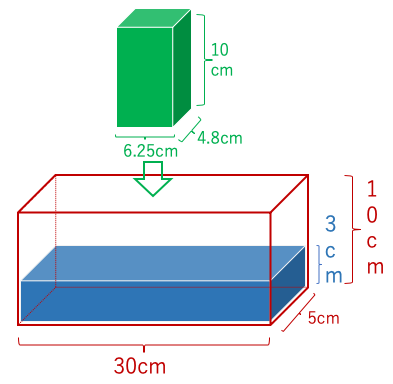
水の体積は30×5×3=450(cm3)
棒を底までつけると底面積は少なくなる。
30×5-6.25×4.8=120(cm)
水の体積を底面積で割ると
450÷120=3.75(cm)
立体模型を活用した中受教材
別解1:
底面積:棒なし=150(cm2)、棒あり=120(cm2)
高さ:棒なし=3cm、棒あり=xcm
高さの比は底面積の比の逆比になる。
底面積の比は150:120=5:4
高さの比は4:5
3×
=3.75(cm)
[下位層の生徒や自閉症の生徒は水量変化を5回説明しても理解できない場合がある。
偏差値40台の中堅校を狙う場合には水量変化の問題に執着する必要はなく、
打ち切って理科に時間を使っても問題ない。]
例題:2つの直方体をくり抜いたた水槽に6cmの水が入っている。
この水槽を横にした時の水の高さは何cmか?
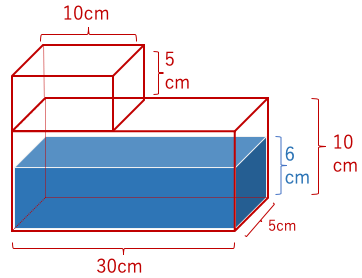
解答:30×5×6÷(10×30+5×10)=2(cm)_答
解説:水槽が縦向きの状態での底面積が30×5、
水の高さが6cmのため30×5×6(cm3)の水が水槽に入っているとわかる。
水槽が横向きの時の底面積は大きい方の直方体の側面積が30×10
小さい方の直方体の側面積が10×5
側面積はその和の(10×30+5×10)なので、水の体積30×5×6を側面積で割ると水面の高さが2cmとわかる。
Short Notes
Homeに戻る