Short Notes

確率分布

概念が難しいが、概念を解説、回答している動画を何個か見ればうっすらと理解できる。
出題パターンが少なく共通テストでも数列、ベクトルを選択するより、少ない時間で完答しやすく計算ミスをしにくい。
２次試験では出題範囲から外されていることも多いが、新課程の数学Bでは必須化される。
標準正規分布への標準化や公式の暗記が多少難しいが、
１５時間程度で完成する。数列から逃げたい生徒から好評の分野。
(理工学系大学院入試の範囲に入る場合がある)

【現役東大生・早慶生による学習管理コーチング】難関大学・難関高校合格のための個別指導塾

二項分布

二項分布：binomial distribution
試行の結果が二種類p,1-p
独立にn回試行したときに、
事象Aの発生回数Xが従う確率はB(n,p)
P(X=k)=_nC_kp^k(1-p)^n-k
E[X]=np
V[X]=np(1-p)
δ(X)=

\sqrt{V(X)}

=

\sqrt{np(1-p)}

(備考：参考書に関連話題として出る場合もあるが、試行回数が1の二項分布がベルヌーイ分布)

標準正規分布

平均0,分散１になる確率分布。
後述する分布は全てこの標準正規分布に標準化される。

正規分布

正規分布：normal distribution
平均m,分散δ²でN(m,δ²)
xをZ=

\frac{x-平均}{標準偏差}

として
N(0,1)に標準化する。

母平均の推定

調べたい集団全体を母集団とする。
母集団の平均がわからないor調べられない時、母集団の平均を抜き取った標本(サンプル)から母平均を推定する。
95%の確率で~~から--の間に収まるはずだと
母平均mに対する信頼度95%の信頼区間

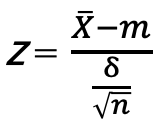に従う。

\overline{X}

:標本平均
Z：標準正規分布に標準化された確率変数
m:X(母集団)の平均値
δ:X(母集団)の標準偏差
n:抽出した標本のサンプル数
サンプル数が大きくするほど、信頼区間の幅を狭くすることができ、精度の高い推定ができる。
信頼区間95%の場合、

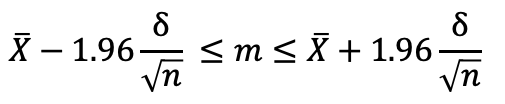
確率が正と負でそれぞれ0.4750ずつ(z=1.96)
信頼区間99%の場合

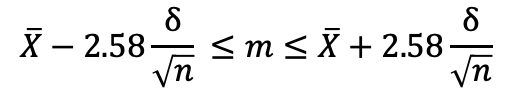
確率が正と負でそれぞれ0.49506ずつ(z=2.58)

99%信頼区間とは？
[母集団から標本を取得し、その標本の平均から99%信頼区間を求める
操作を100回行ったとき99回はその区間の中に母集団の平均値が含まれる]
という意味。

母比率、標本比率

母集団の中で事象Aが発生する確率が母比率
標本の中で事象Aが発生する確率標本比率R

↑具体例：母集団に不良品が混じっているとし、不良品の割合を調べるとする。
母集団から何個か取ってきて標本をつくる。
標本の中で不良品の個数を調べX個とわかるとする。
R=

\frac{X}{n}

標本比率とする。
Xは二項分布B(n,p)に従い、nが大きいときXは正規分布に従う。
R=

\frac{X}{n}

も近似的に
正規分布N(p,

\frac{p(1-p)}{n}

)に従う。
[参考：N(平均,分散)]

母集団の中で特定の性質αをもつ個体の割合をpとする。
pを性質αをもつ個体の母集団における母比率という。
大きさnの標本を母集団から抽出したとき、この標本において性質αをもつ個体の割合p₀より母比率を推定すると
母比率pに対する信頼度95%の信頼区間pは

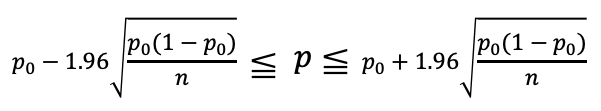
母比率pに対する信頼度99%の信頼区間pは

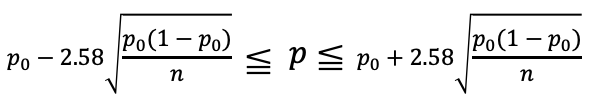
確率密度関数

確率密度関数f(x)のように確率が関数で表せる。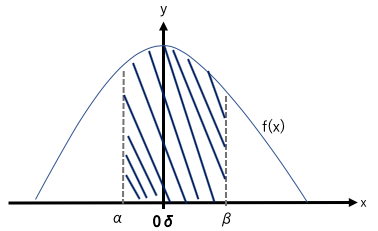

平均：

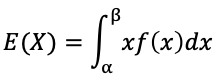
分散：

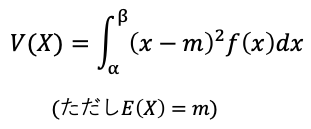
リンク

Short Notes