式と曲線

楕円

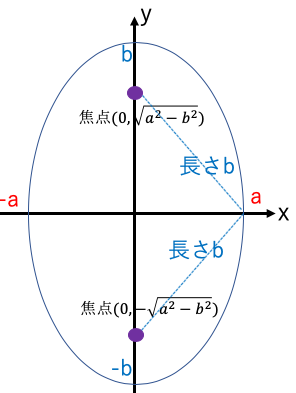
a>bのとき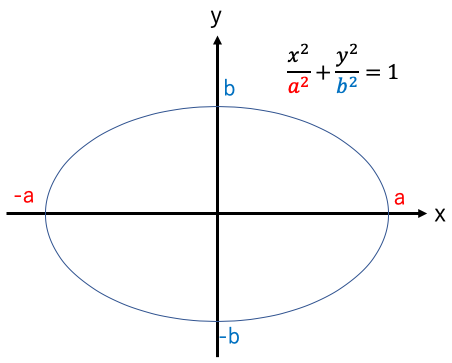

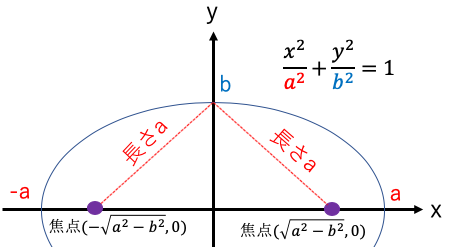
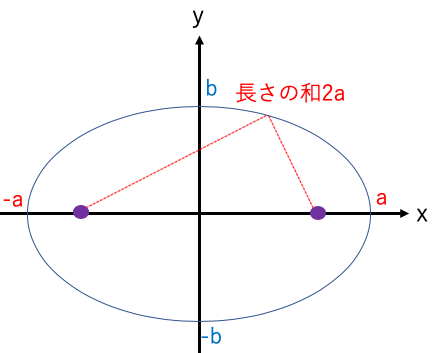
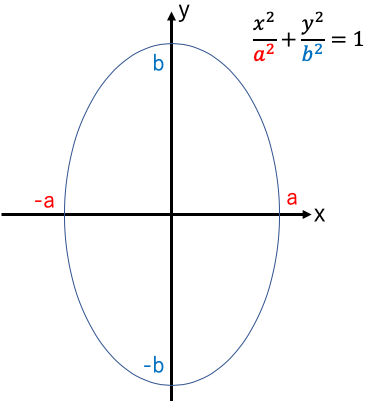
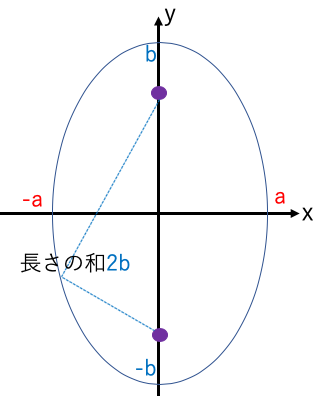
a< bのとき

双曲線とは：焦点と双曲線上の座標間の２本の線分の差が2aになる。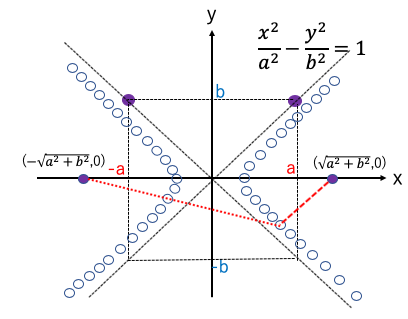

２本の赤線の長さの差が2aになる。

双曲線の焦点：

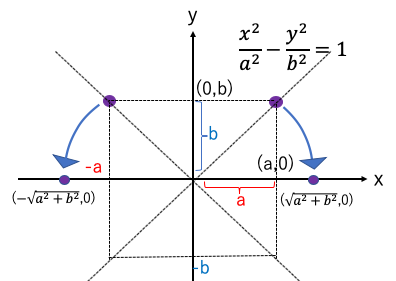
焦点のx座標はx²=a²+b²から算出した。

-----------------------------------------------------

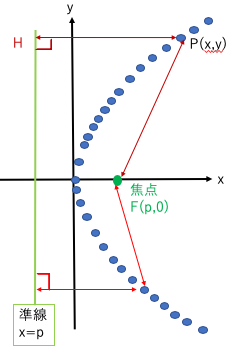
焦点(p,0),準線x=-p
赤茶色の距離は等しい。(PH=PF)また、赤線の距離も等しい。

接点を(x₁,y₁)とすると各図形の接線は
楕円：

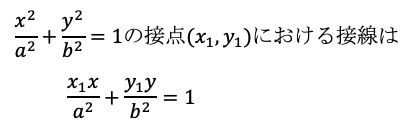
双曲線：

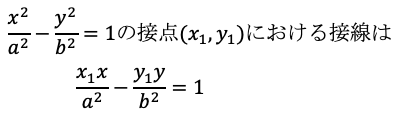
放物線：y²=4pxの接線は
y₁y=2p(x+x₁)
と少しx₁の位置が特殊である。

直交座標だと(x,y)で表現していた図形を、
極座標では図形上の点を(r,θ)とおいて図形を表現する。

焦点-図形上の点の距離と図形上の点-準線の間の比率を1:eとすると、eが離心率。

離心率が0 < e < 1：楕円になる。
離心率１：放物線。
離心率が１< e：双曲線
(離心率：心(焦点)から離れる割合。)
(e = 0だと円とみなす。)

Short Notes