積分(数学3)

不定積分公式

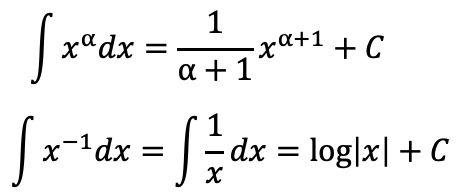
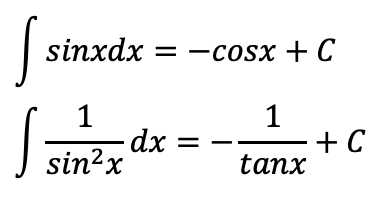
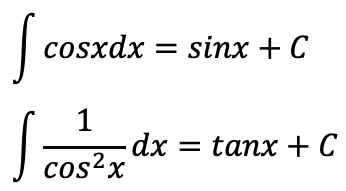
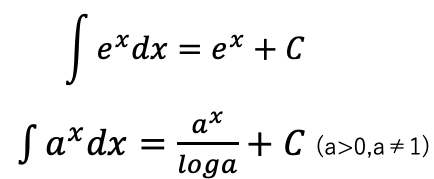
置換積分(不定積分)

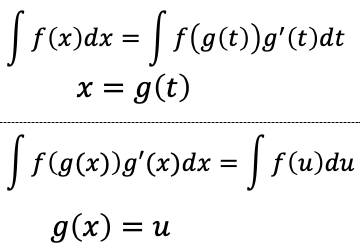
部分積分

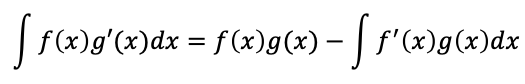
定積分の性質

(1)定積分
f(x)の原始関数の１つをF(x)とするとき

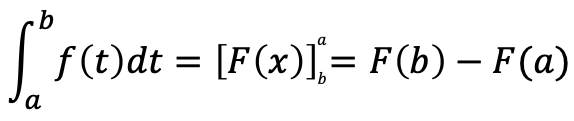
(2)定積分の性質
(A)

(B)

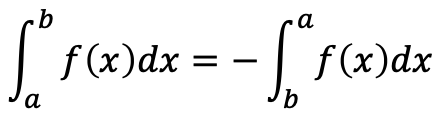
(C)

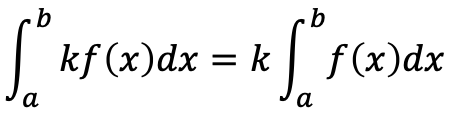
（k：定数）

(D)

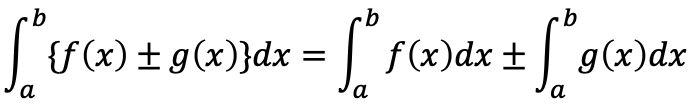
(複合同順)

(E)

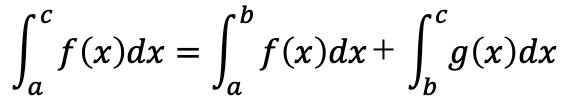
(3)偶関数と奇関数の定積分
(A)f(x)が偶関数のとき

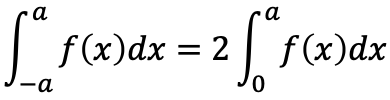
(B)f(x)が奇関数のとき

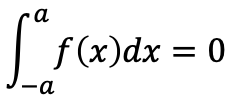
置換積分(定積分)

区間[a,b]において関数f(x)は連続であり、
xが区間(a,b)で微分可能な関数g(t)を用いてx=g(t)と表される場合
a=g(α),b=g(β)のとき

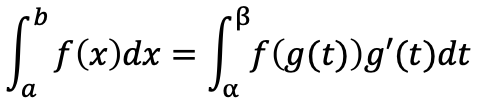
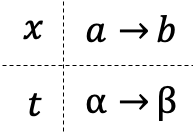
微分と積分の関係

定積分の部分積分法

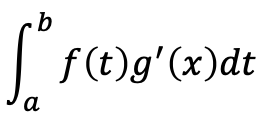
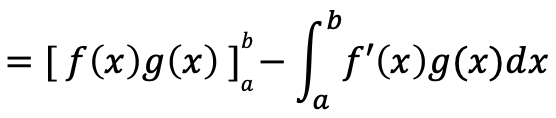
微分と積分の関係

(A)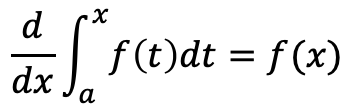

(aは定数)

(B)

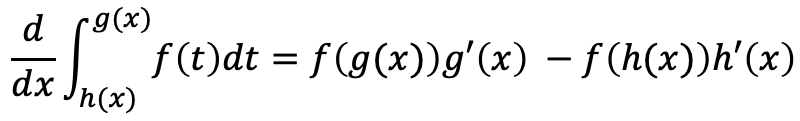
定積分と区分求積法

区間を細かく分け、和の極限値としての面積や体積を求積する方法。
f(x)が閉区間[a,b]で連続のとき、この区間をn等分し、
その分点をa=x₀,x₁,....,x_n,x_n-1=b
とすると

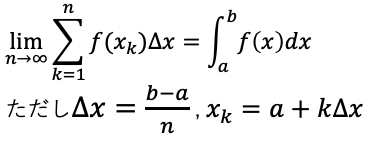
とくにa=0,b=1のとき

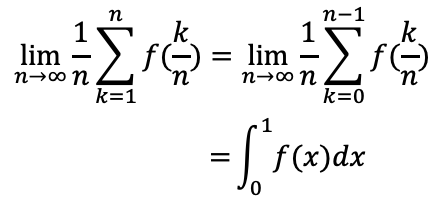
定積分と不等式

区間[a,b]で連続な関数f(x)、g(x)において
(A)区間[a,b]においてつねにf(x)≧0ならば

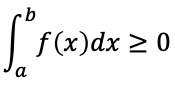
f(x)=0のときに限る。

(B)区間[a,b]で常にf(x)≧g(x)ならば

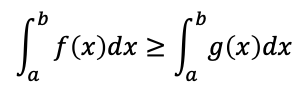
等号が成り立つのは常にf(x)=g(x)のときに限る。

２曲線で囲まれた図形の面積

区画[a,b]においてf(x)≧g(x)であるとき
2曲線y=f(x),y=g(x)と２直線x＝a,x=b
にて囲まれた図形の面積Sは

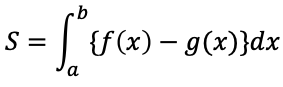
y軸と曲線で囲まれた図形の面積

区画c≦y≦dにおいてf(y)≧0であるとき
曲線x＝f（y）とy軸および２直線y=c,y=dで囲まれた図形の面積Sは

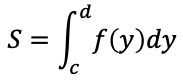
体積

立体をx軸に垂直な平面で切断したときの断面積がS(x)である立体の体積Vは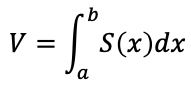

回転体の体積

(A)x軸のまわりの回転体の体積
曲線y=f(x)とx軸および２直線x=a,x=b(a<　b)で囲まれた図形をy軸の周りに１回転してできる回転体の体積Vは

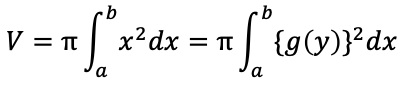
(B)y軸のまわりの回転体の体積
曲線y=g(y)とy軸および２直線y=c,y=d(c< d)
で囲まれた図形をy軸のまわりに１回転してできる回転体の体積Vは

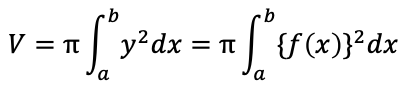
曲線の長さ

(A)媒介変数表示された曲線
x=f(t),y=g(t)(a≦t≦b)
の長さをLとすると

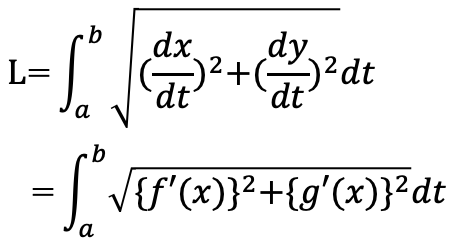
(B)曲線y=f(x)(a≦t≦b)の長さをLとすると

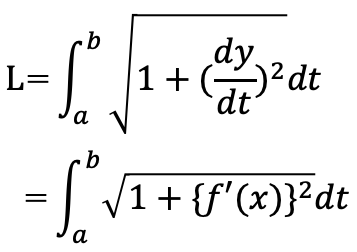
速度と道のり

(A)数直線上の運動
点Pの時刻tにおける座標をx=f(t),y=g(t)と表されるとき,
t=a,t=bまでに点pが通過する道のりlは

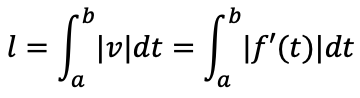
(B)平面上の運動
点Pの時刻tにおける座標(x,y)が
と表されるとき
t=aからt＝bまで点Pが通過する道のりlは

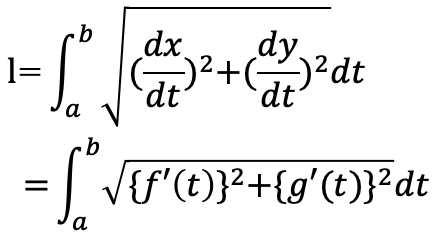
点Pの速度をと表すと

-----------------------------------------------------

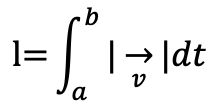
Short Notes