数と式
レパートリーが多く、覚えるパターンや応用問題が多彩。ある意味最難関分野。この分野の基本パターンの変形はサラッとできるようにしたい。
主な因数分解の公式
(x+y)2=x2+2xy+y2(x-y)2=x2-2xy+y2
二重根号
==
帝都大学へのビジョン
命題と論理
論理分野の基礎の習得はさほど難しくない。とても簡単なドモルガンの法則を理解できず、使いたがらない生徒が多い。
ドモルガンや対偶や背理法はロジックを理解せずにパターン的に適用しても問題ない。
(理工学系大学院入試の範囲に入る場合がある)
ドモルガンの法則
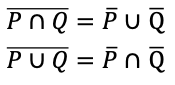
[上線は否定。]
否定の上線を分けて記号を逆に変えるだけである。
背理法
命題が正しくないと仮定して矛盾を導き、命題が正しいと証明する手法。対偶
P→Qが証明しにくい場合に対偶で¬Q→¬Pを証明する。
循環小数
例題:x=8.181818181...のような循環小数を分数で表せ。100X=818.8181818...を作り、小数点以下を消去できるように
100x-xを計算すると
99x=810となり
x=と表せる。

Short Notes
Homeに戻る