微分積分
基礎概念でわかりにくい箇所はほとんどなく、二次関数を微分すると接線になるという概念が少し理解しづらく戸惑う。
積分の手順を暗記し、上の関数から下の関数を引くだけの浅い分野。計算が大変。
計算力があれば応用問題も普通に回答できる。
京大などの上位校の入試本番では最も得点が安定しやすい微積から回答することが多い。
微分
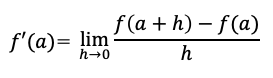
↓位置を微分すると速度が分かる例
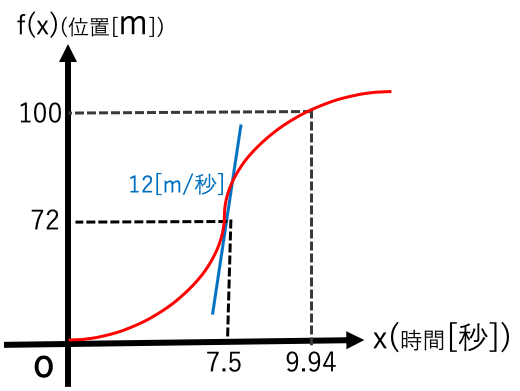
上記グラフでは7.5秒(72m地点)で最高速度に達したことがわかっているとする。
x(時間)でグラフの関数(位置)を微分しx=7.5を代入すると傾きf'(7.5)=12となる。
したがって速度速度は12m(=時速43.2km)と分かる。
積分
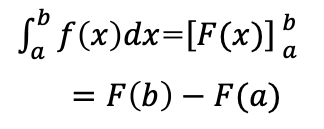
微分の図と同様に
100m走の選手が7.5秒で速度のピークを迎え9.94秒でゴールしたデータのf(x):速度、x:時間(秒)のグラフ
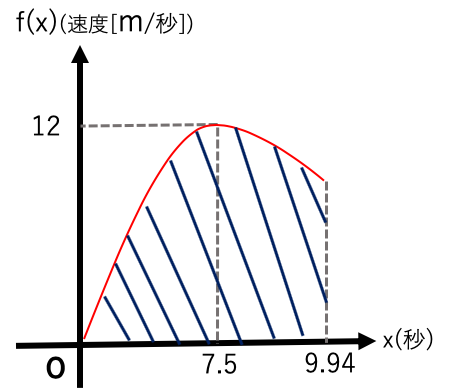
紺色の斜線の面積が100(m)になる。
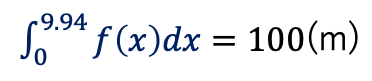
速度を積分すると走った距離になる。
リンク
Short Notes
Homeに戻る