複素数

共益な複素数の性質

複素数a+biについてa-biを共役な複素数という。
z=a+biとすると、共役な複素数は
z=a-bi
と表す。

zの共役な複素数zの共役な複素数はzと一致する。

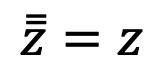
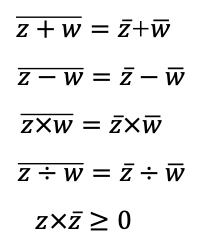
複素数の絶対値

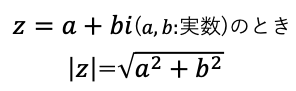
複素数の極形式

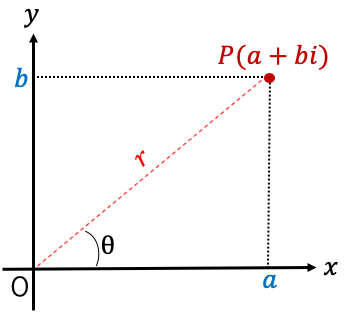
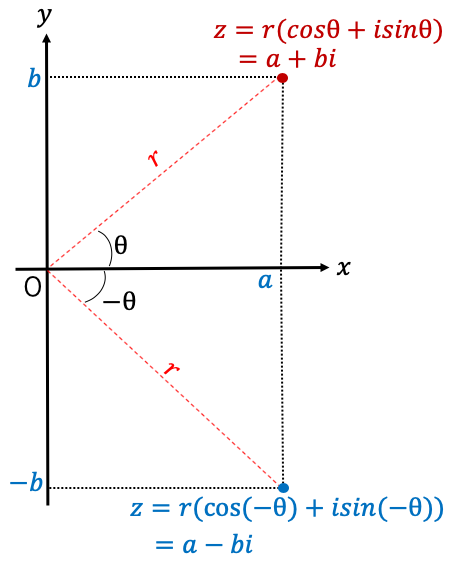
z=a+biのとき、上の図からa=rcosθ,b=sinθとなり、
r>0となる。
z=r(cosθ+isinθ)と「極形式」で表記できる。
θをzの偏角を定義しargz＝θで表す。
r=|z|

a+biの共役な複素数a-biを極座標考える。
a-bi=r(cosθ-isinθ)

a-biを座標平面上に図示すると。

複素数の積と商

z₁=r₁(cosθ₁+isinθ₁)

z₂=r₂(cosθ₂+isinθ₂)

z₁×z₂=r₁r₂
=(cos(θ₁+θ₂)+isin(θ₁+θ₂)
・・・①
z₁÷z₂=

\frac{r1}{r2}

(cos(θ₁-θ₂)+isin(θ₁-θ₂)
・・・②

（備考）
①証明
z₁×z₂ =r₁(cosθ₁+isinθ₁)×r₂(cosθ₂+isinθ₂)
=r₁r₂(cosθ₁cosθ₂+cosθ₁isinθ₂+isinθ₁cosθ₂+isinθ₁isinθ₂)}[展開した]
=r₁r₂(cosθ₁cosθ₂-sinθ₁sinθ₂)+i(sinθ₁cosθ₂)+cosθ₁sinθ₂}[実部と虚部に加法定理を適用]
=r₁r₂ (cos(θ₁+θ₂)+isin(θ₁+θ₂)

②証明
z₁÷z₂
=

\frac{r1}{r2}

\frac{(cosθ1+isinθ1)(cosθ2-isinθ2)}{(cosθ2+isinθ2)(cosθ2-isinθ2)}

[分母分子に(cosθ₂-isinθ₂)をかける]
(分子)==r₁{(cosθ₁cosθ₂+sinθ₁sinθ₂)+i(sinθ₁cosθ₂-sinθ₁cosθ₂)
(分母)=r₂(con²Θ₂+sin²Θ₂)
=r₁cos(θ₁-θ₂)+isin(θ₁-θ₂)

ド・モアブルの定理

(cosθ+isinθ)ⁿ=cosnθ+isin nθ

1のn乗根

zⁿ=0の１つの解を１のn乗根と言われ以下の式が成り立つ。

zⁿ=cos(

\frac{2π}{n}

×k)+isin(

\frac{2π}{n}

×k)
(k=0,1,2,...,n-1)

複素数と角

点B(β)を点A(α)を中心として反時計周りにθ回転した点C(γ)は
γ=(cosθ+isinθ)(β-α)+α
→

\frac{γ-α}{β-α}

＝cosθ+isinθであるから
θ=

\frac{γ-α}{β-α}

２直線のなす角は

\frac{γ-α}{β-α}

を極形式で表せばわかる。

一直線上にある条件,垂直に交わる条件

３点が一直線上にある条件。
複素数平面上の３点A(α),B(β),C(γ)について
角BAC=arg(

\frac{γ-α}{β-α}

)
３点A,B,Cが一直線上にある条件は、
角BAC=0度か角BAC=180度
なのでsin0＝0か、sinπ＝0となる。
複素数

\frac{γ-α}{β-α}

の虚部が0となり、実部だけとなる。

\frac{γ-α}{β-α}

が実数となる。

３点AB,ACが垂直になる条件は、
角BAC=

\frac{π}{2}

となり、
なのでcos

\frac{π}{2}

＝0となる。
複素数

\frac{γ-α}{β-α}

の実部が0となり、虚部だけとなる。

\frac{γ-α}{β-α}

が純虚数となる。

-----------------------------------------------------

Short Notes

Homeに戻る