数の性質

--------------目次(公約数)---------------
公約数/公約数,公倍数の算出法
--------------目次(分数)---------------
分母と分子の和と差/単位分数
部分分数分解
-----------------------------

公約数

1以上の整数Aと1以上の整数Bがあり、
AがBで割り切れる時、 BをAの約数と言う。
20の約数:1,2,4,5,10,20
30の約数:1,2,3,5,6,10,15,30
２つ以上の整数に共通な約数をそれらの整数の公約数と言う。
20と30の公約数は1,2,4,5,10である。
公約数の中で最も大きい数を最大公約数と言う。
20と30の最大公約数は10である。

１からxまでの整数の中にあるyの倍数の個数はx÷yの商で求められる。
例題：１から１００の間に８の倍数は何個あるか？

100÷8=12あまり4
12個_答え

公約数,公倍数の算出法

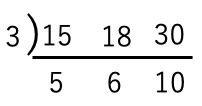
公約数は数字１つが割り切れなくなると連除法を打ち切る。
)の左の数の積が最大公約数
3が最大公約数

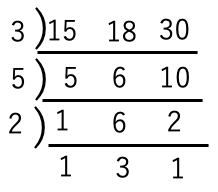
公倍数を求める場合には数字一つが割り切れない場合でも、
他の二つ以上が割り切れる場合は連除法を継続する。
)の左と-の下の数の積が最小公倍数
ここでは3×5×2×1×3×1
の90が最小公倍数

算数塾の個別指導

分数

分母と分子の和と差

分母と分子の差が48であり、約分すると

\frac{5}{13}

になる分数を求めよ。

解答：
約分すると

\frac{5}{13}

になる分数は

\frac{5×z}{13×z}

(z:整数)とおける。

分母と分子の差は４８であるので、
13×z-5×z=48

→8×z=48

→z=6

よって求める分数は

\frac{5×6}{13×6}

\frac{30}{78}

答え

かけて整数になる分数

分数

\frac{y}{x}

に

\frac{34}{6}

をかけても

\frac{85}{7}

をかけても整数になるとき、
このような分数の中で最も小さい数をもとめなさい。

\frac{y}{x}

\frac{34}{6}

\frac{y×34}{x×6}

より

y:6の倍数、x:34の約数とわかる。

\frac{y}{x}

\frac{85}{7}

\frac{y×85}{x×7}

より
y:7の倍数、x:85の約数とわかる。

分子y:小さい方が良い
分母x:大きい方が良い

x:85と34の最大公約数→17
y:6と7の最小公倍数→42

\frac{42}{17}

\frac{8}{17}

単位分数

例題：

\frac{1}{x}

\frac{1}{y}

\frac{1}{z}

\frac{11}{18}

答え
を求めよ。(x<　y　<　zとする)

分母の18の約数は18,9,6,3,2,1
分子は11のため11を約数の中で３つの数の和で表す。
2+3+6=11

\frac{2}{18}

\frac{3}{18}

\frac{6}{18}

\frac{1}{9}

\frac{1}{6}

\frac{1}{3}

よりx=2,y=3,z=6

部分分数分解

以下の□を求めよ。

\frac{1}{20}

\frac{1}{30}

\frac{1}{42}

+ .......+

\frac{1}{110}

=□

→(左辺)＝

\frac{1}{4×5}

\frac{1}{5×6}

\frac{1}{6×7}

+ .......

\frac{1}{10×11}

→(

\frac{1}{4}

\frac{1}{5}

)+ +(

\frac{1}{5}

\frac{1}{6}

)+ +(

\frac{1}{6}

\frac{1}{7}

)+ .......+(

\frac{1}{10}

\frac{1}{11}

)
=

\frac{1}{4}

\frac{1}{11}

\frac{11}{44}

\frac{4}{44}

\frac{7}{44}

□＝

\frac{7}{44}

Short Notes

Homeに戻る