案外早くに偏差値50ボーダーには到達できるので保護者や学生講師予習して教えても十分キャッチアップできる。
ただ高校受験組の講師は予習を嫌がる傾向にある。
-------------------------------------------
和差算/ 分配算
平均算/ つるかめ算
倍数算/ 損益算
相当算/ 年齢算
ニュートン算/ 濃度算
差集め算/ 植木算
過不足算
-------------------------------------------
和差算
例題1:あるクラスの人数は40人であり、
マスクをしている人はしていない人より10人多い。
このクラスでマスクをしている人の人数は何人か?
解説動画
解答:
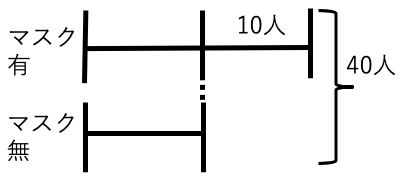
(マスク有人数)=(40-10)÷2+10
=25(人)
<中学受験>子どもが自分から机に向かうようになる秘訣
例題2:
あるオーストラリアの語学学校の人数は50人であり、
中国、韓国、日本人で占められている。
中国人は韓国人より10人多く、
日本人は韓国人より2人少ない
日本人は何人か?
解説動画:
解答:
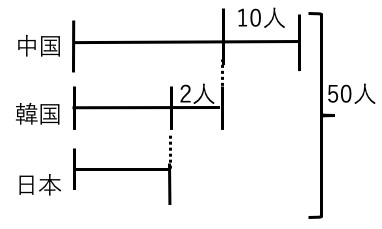
日本人との差を表すと
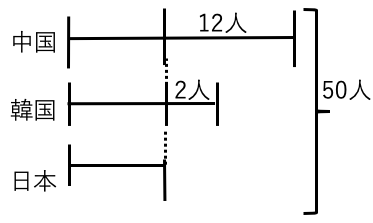
(日本人の人数)={50-(12+2)}÷3
=12(人)
算数塾の個別指導
分配算
例題3:夫婦で車で交代で運転しながらオーストラリアを一周しました。
一周には9500kmかかりました。
夫は妻の2倍より500km多く運転しました。
妻が運転した距離は何kmでしょう?
解説動画:
解答:
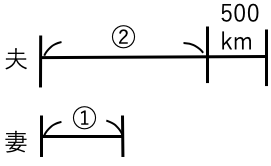
妻の運転距離は①
①=(9500-500)÷3 =3000(km)
例題4:
日本人の佐藤くん、中国人の江くん、韓国人の李君がオーストラリアの農場でクランベリー狩りをしていました。
3人でクランベリーを500個取りました。
江君は佐藤君の二倍クランベリーを取り、李君は佐藤君の3倍から40個少ない数のクランベリーを狩りました。
佐藤君は何個のクランベリーを取ったでしょうか?
解答4:
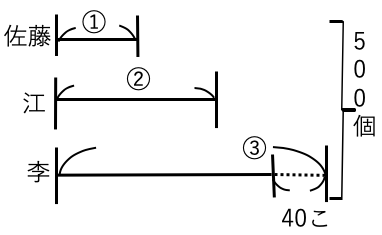
①+②+③=500+40
⑥=540
①=90
佐藤君は90個クランベリーを取った。

平均算
例題5:オーストラリアの語学学校の下位クラスで日本人20人のTOEIC平均450点外国人の平均点が600点、
クラスの平均点は540点であった。
このクラスに外国人は何人いますか?
解答5:
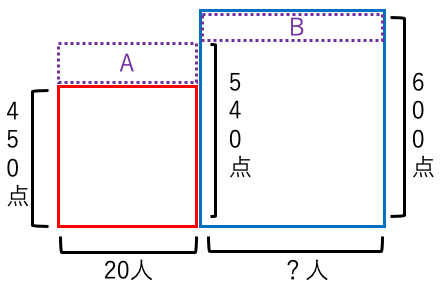
図中の紫の長方形Aと長方形Bの面積は等しくなる。
(540-450)×20=(600-540)×(外国人の人数)
1800=60×(外国人)
外国人は30人いるとわかる。
例題6(平均算):
40人のクラスで算数のテストを行うと、
男子の平均点は58.2点、女子の平均点は60.2点でした。
クラス全体の平均点が59点でした。
このときの女子の人数を求めなさい。
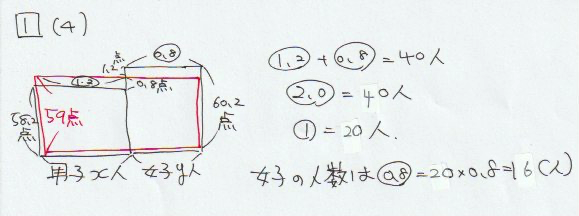
つるかめ算
例題7:32才男性が2022年のアメリカで一玉700円のレタスと一つ400円のカップ麺を合わせて10個買ったら、
代金は5250円でした。
男性はカップ麺を何個買いましたか?
解答7:
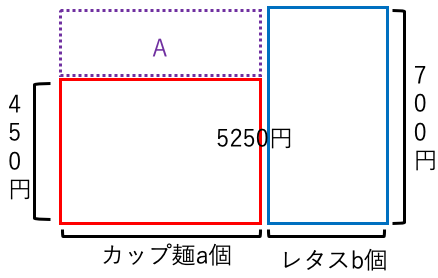
10個×700円-5250円=(紫の長方形A)
(紫の長方形A)=250×a
a=7(個)
例題8:速さのつるかめ算
節約中のバックパッカーが30kmを分速50m歩き、
途中で安いタクシーを見つけて乗車し、
分速1000mで移動し22分かかって空港に着いた。
タクシーに乗車していた時間は何分か?
解答8:
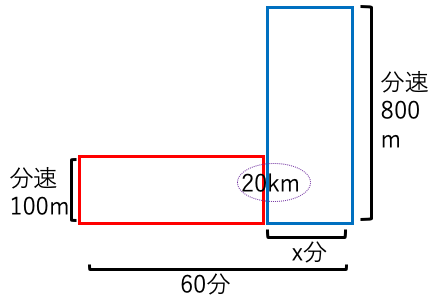
青と赤の長方形を足すと20km(20000m)である。
(赤と青の長方形の面積)=(60-x)×100+x×800
20000=6000-100x+800x
14000=700x
x=20(分)
例題10:3要素のつるかめ算
Aくんがボールペン80円、えんぴつ50円、消しゴム120円を合計50個買ってお金を支払った。
えんぴつと消しゴムの個数が同じ時、ボールペンの本数を求めよ。
(偏差値45中学過去問改題)
解答10:
長方形が3つあると回答しにくいので、2つを1つの長方形にまとめる。
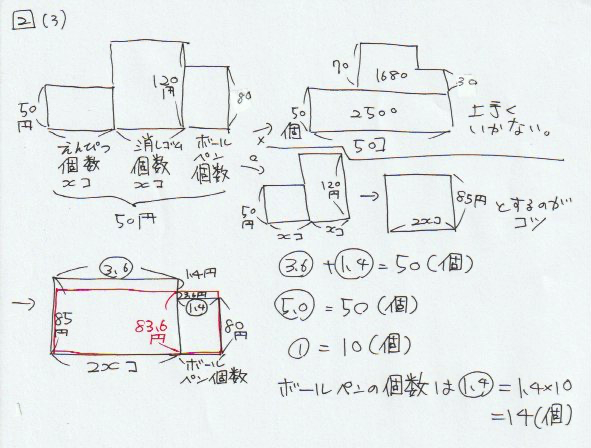
消去算
例題11:スイスでコーラ2本とビッグマック3個を買うと3500円、コーラ4本とビッグマック5個を買うと6100円になる。
コーラ一本の値段は何円か?
解答11:
---------------------------------------
コ×2+ビ×3=3500...①
コ×4+ビ×5=6100...②
①の式を二倍して
コ×4+ビ×6=7000...③
③の式から②の式を引いて
ビ×1=900
これと①より、
コ×2+900×3=3500
コ×2=800
コ=400
コーラは400円
(中学数学の方程式と同様の考え方)
倍数算
例題12:はじめに朝倉とジョリーの所持金の比が29:1でしたが朝倉がジョリーに500万円あげたので二人の所持金の比は9:1になりました。
はじめのジョリーの所持金はいくらですか?
12解答:朝倉がジョリーに500万円をあげても二人に所持金の和は変わらないのがポイント。
お金を渡す前後での二人の所持金の比の和を揃える。
始め:29x:1x
後:9y:1y=27y:3y=27x:3x(和を初めの和との最小公倍数になる)
29x-27x=2xがジョリーに渡した500(万円)にあたるから
x=250(万円)
ジョリーの始めの所持金は250万円_答
例題13
はじめ、こめおと山川の所持金の比は10:1でしたが、
二人ともブレイキングダウンで3250万円稼いだので、
所持金の比は25:22になりました。
初めの山川の所持金は何円でしたか?
13解答:二人は同額稼いでも所持金の差は変わらない。
比の差を最小公倍数の9に揃えると
初め:10:1=10x:1x
後:25:22=75x:66x
65x=3250万円
x=50万円
初めの山川の所持金は50×1=50(万円)_答え
[倍数算はノウハウは難しくないが、入試問題に混ぜられると誤った数直線を書いたりして、
回答できない生徒が多い(数直線を利用しても回答できる。)]
損益算
例題14:原価800円の品に3割の利益を見込んで定価を付けたが、売れ残ったため、定価の2割を引いて売りました。
売れたときの利益は何円か?
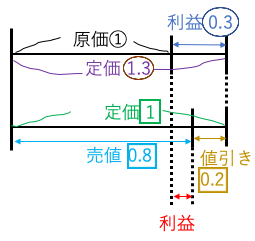
解答14:
①:(1)、□1:[1]としている↓
解答:原価を(1)とする。
定価は(1)+(0.3)=(1.3)にあたる
定価は800×1.3=1040(円)
定価を[1]とすると
売値は[1]-[0.2]=[0.8]にあたる
売値は1040×0.8=760(円)
利益は1040−760=280(円)
相当算
例題15:一日目は全体の半分を読み、2日目は残りのを読んだのに残りは35ページになった。
この本は全部で何ページあるか?
解答15:
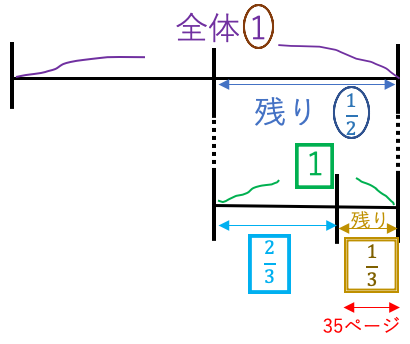
①:(1)、□1:[1]としている↓
本のページ数を(1)とすると
1日後の残りページ数は(1)-()=()
1日目の残りのページ数を[1]とすると
2日目の残りぺージ数は[1]-[]=[]
これが35ページに当たるので、
[1]に当たる1日目の残りページ数は35÷=105
これが()に当たるので、
105÷=210(ページ)
年齢算
例題16:現在、ガクトは49才、ひかぴーは16才です。ガクトの年齢がひかぴーの年齢の2倍になるのは何年後か
解答16:
二人の年齢差が□年後も変わらないことがポイント。
現在から□年後のひかぴーの年齢を①とすると,
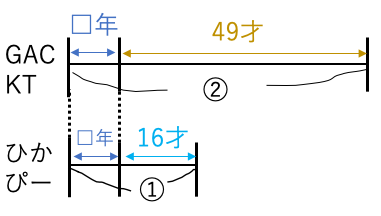
その際のガクトの年齢は②です。
①が49-16=33才にあたるから
□=33-16
□=17(年後)
ニュートン算
例題17:シドニーでははじめにある程度の日本人限定の仕事の求人があり、一日ごとに同じ数の日本人求人が発生する。
新しい日本人が30人増えると6日で仕事の募集はなくなる。
日本人が40人増えると4日で仕事の募集はなくなる。
日本人が50人増えたとき、日本人の求人は何日でなくなるか?
【中学受験専門】個別指導塾ドクター
中学受験専門のプロ講師集団(元SAPIX・日能研・四谷大塚の講師)が運営しています。
これらのプロが直接ご相談をたまわり、オーダーメイドにて
お子様に合った受験学習を個別指導。
解答17:
①:1日で増える求人数
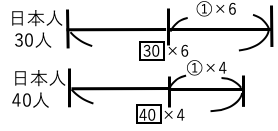
30人増えた場合:[30]×6+①×6=[180]+⑥
40人増えた場合:[40]×4+①×4=[160]+④
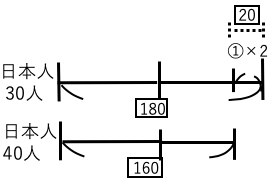
上の数直線より
②=[20]
①=[10]
a:1日に50人増えた場合に求人が埋めるのにかかった日数。
新しい日本人が50人増えた場合以下の図のようになる。
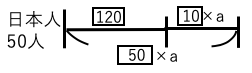
120+[10]×a=[50]×a
120=[40]×a
a=3
3日で日本人の求人はなくなる。
(備考:オーストラリアで英語が喋れない日本人は違法賃金の和食店(通称;ジャパレス)で働かざるを得ない。)
中学受験 社会・理科 脳プレス高速暗記講座 社会三編理科セット
濃度算
例題18:500gの食塩水を□g蒸発させると10%の食塩水になった。□の数字を答えよ。解答18:
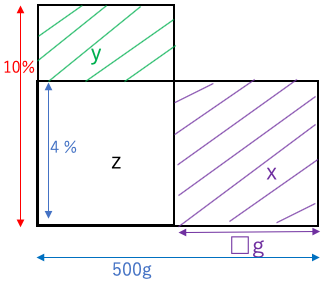
x+zとy+zの長方形の面積
x+z:500(g)×4(%)=2000
y+z:10(%)×500-□(g)=5000-10×□
x+z=y+z+yより
2000=5000-10×□
→2000+10×□=5000-10×□+10×□
→2000+10×□=5000
→2000+10×□-2000=5000-2000
→10×□=3000
→□=300(g)答
(面積は塩の量である。縦長の長方形と横長の長方形の面積は等しい[同じ塩の量20gのため]。)
同じ量のモノが2つあると上記の面積図になる。
(□が増えると方程式が複雑になるため、面積図や天秤図偏差値55レベルの中学受験生でも処理は厳しい。)
差集め算
例題19:ある本を毎日18ページで読むと12ページ読むより9日早く読み終わる。この本は何ページあるか?
リンク
解答19:
縦をページ数、横を日数とした面積図
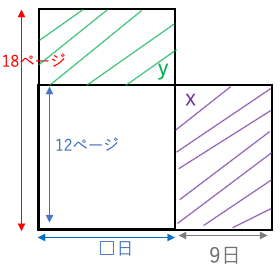
x:12(ページ)×9(日)
y:(18-12)(ページ)×□(日)
x=yのため
(18-12)×□=9(日)×12(ページ)
□=18(日)
本のページ数は 18ページ×□(日)なので
18×18=324(ページ)_答え
(縦長の長方形[18ページ×□日]の面積は本のページ数、
横長の長方形[12ページ×(□+9日)]の面積も同一の本のページ数)
差集め:例題20:Aくんは1コ260円のケーキを何個か買う予定でケーキ屋さんにいきましたが、
全て売り切れだったので、代わりに1コ300円のケーキを買いました。
すると予定の金額では、買うつもりだった個数より2コ少なくなりました。
1コ260円のケーキを何コ買う予定でしたか?
(偏差値45中学過去問)
リンク
解答20(1):差集め算面積図
差集め算の面積図を書こうと思うと
2個数を少ない方の個数(ここではx-2個)に揃えることに注意せねばならず、作図は案外手間取る。
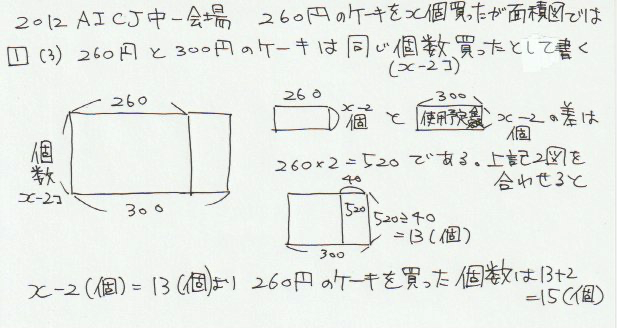
解答(2):
使用予定金額が260の場合も300の場合も同額のため、濃度算の面積図を使用しても良い。
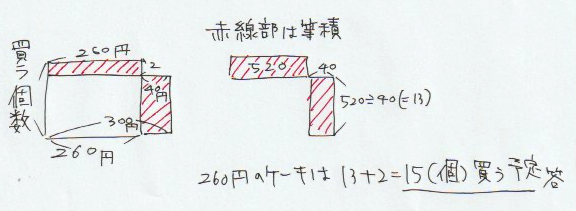
植木算
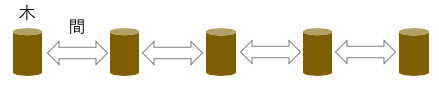
両端に木を植える:木の本数=間の数+1
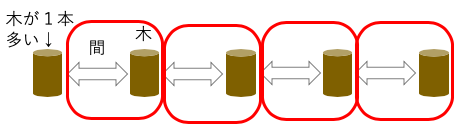
↑間と右の木をワンセットで考えると楽。
両端に木を植えない:木の本数=間の数-1
(植木算では端の木または間の処理がポイント。)
右端か左端に木を植える:木の本数=間の数
例題21:100mの道路の片側に木を植える。端から端まで4m間隔で植えると木は何本必要か
解答21:100÷4=25
25+1=26(本)
過不足算
例題22:ジュースを小学生□人に配る。一人5Lずつ配ると4L余る。
一人8Lずつ配ると11L不足する。
□に当てはまる小学生の人数は何人か?。
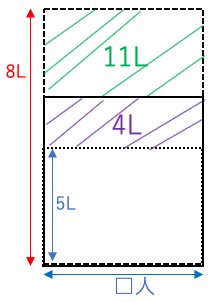
解答22:
斜線部の縦の長さが3(L)で面積が11+4=15(L)の長方形に注目する。
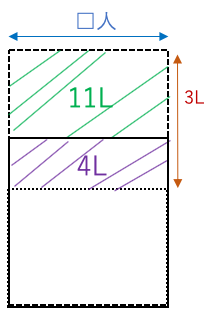
縦の長さが3(L)のため
長方形の横の長さ□人は
15÷3=5(人)
答え_小学生は5人
-------------------------------------------
和差算/ 分配算
平均算/ つるかめ算
倍数算/ 損益算
相当算/ 年齢算
ニュートン算/ 濃度算
差集め算/ 植木算
過不足算
-------------------------------------------
Short Notes
Homeに戻る