展開
パターン１：(x+a)(x+b)=x2+(a+b)x+a×b以下の式も暗記した方が良い。
パターン２：x2+2xy+y2=(x+y)2
パターン３：
yに-yを入れると以下の式ができる。
x2-2xy+y2=(x-y)2
x2-y2=(x+y)(x-y)
パターン４：(x+y)(x-y)
=x2-y2
応用パターン
(a+b-c)(a-b+c)
={a+(b-c)}{a-(b-c)}
=(a+X)(a-X)
=a2-X2
=a2-(b-c)2
=a
因数分解
因数分解とは足し算や引き算の式を掛け算の式に変形すること。x2+(a+b)x+a×b
=(x+a)(x+b)
例：x2+7x+10=0を因数分解する場合
足して７かけて１０になる二つの数を考える。
共通因数でくくる。
x4y2+x3yを因数分解する場合
x3yが共通因数のため、
x3y(xy+x)
と因数分解できる。
速音聴で学ぶ中学歴史の簡単学習法
応用編
たすきがけ、 次数整理の２パターンは難しい問題集に掲載されている。いずれも高校の数学１の範囲だが理解しておくと
中学内容で詰まった時の保険になる。
また、高校でも使えるのでコスパがよい。
(過去問で出題されない場合は応用パターンは習得しなくていよい)
応用パターン１：たすきがけ
2x2+6x-20を因数分解する。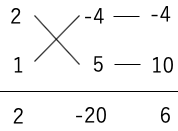
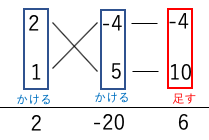
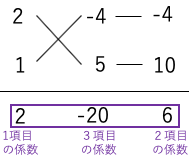
2x2+6x-20
=2x2+6x-20
=2(x+5)(x-2)
応用パターン２：次数で整理
x2y+xyz-y2x-y2z-zx2-z2x+xyz+yz2=(y-z)x2-(y-z)2x-yz(y-z)-yz(y-z)
[xを変数,他を定数と考え、x2,xの一乗,定数の順に整理する。]
=(y-z){x2-(y-z)x-yz}
=(y-z)(x-y)(x+z)
y,zを変数だと考えても整理しても良い。
[中堅高でも他のパターンが複合されているため良い練習にはなるが、
無理に完答できなくとも良い。(高校一年内容では使う。)]
高額塾無用・大学受験合格シンプル勉強法【一粒メソッド】
Short Notes
Homeに戻る