微分
かけ算,わり算の導関数
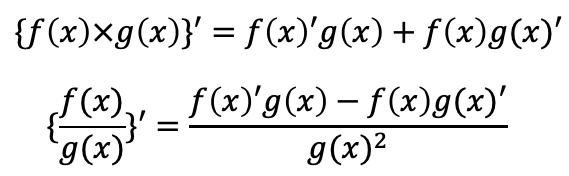
合成関数の微分
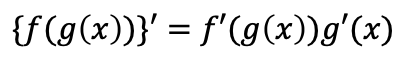
=×
y=(x2+2x+3)3のとき
y'={(x2+2x+3)3}'
→y'=(2x+2)×3(x2+2x+3)2
逆関数の微分
y=f(x)の逆関数をy=f-1(x)とするとx=f(y)
両辺をxで微分すると
1=×
よって1=×
媒介変数で表された関数の微分
x=f(t),y=g(t)のとき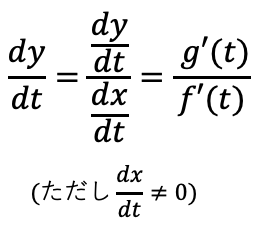
他の導関数
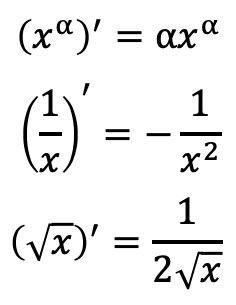
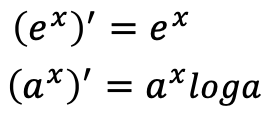
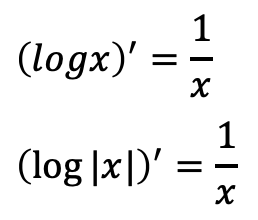
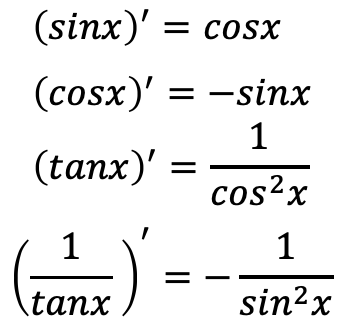
接線、法線の方程式
曲線y=f(x)上の点(a,f(a))における接線の傾きはf'(a)であるから(1)接線の方程式はy-f(a)=f'(a)(x-a)
(2)法線(接線に垂直な直線)の方程式は
f'(a)≠0のとき y - f(a)= - (x-a)
f'(a)=0のとき x=a
平均値の定理
[1]関数f(x)が閉区間[a,b]で連続、開区間(a,b)で微分可能のとき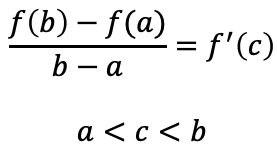
を満たす実数cが存在する。
[2]関数f(x)が閉区間[a,a+h]で連続、開区間(a,a+h)で微分可能のとき
f(a+h)=f(a)+hf'(a+θh)
0 < θ < 1
を満たす実数θが存在する。
導関数の符号と関数の増減
(1)関数の増減関数f(x)が、区間[a,b]で連続、区間(a,b)で微分可能の場合。
(A)区間(a,b)で常にf'(x)>0ならばf(x)は区間[a,b]で増加。
(B)区間(a,b)で常にf'(x)< 0ならばf(x)は区間[a,b]で減少。
(C)区間(a,b)で常にf'(x)=0ならばf(x)は区間[a,b]で一定。
(2)関数の極大・極小
(A)f(x)がx=aを境界にして増加から減少に変化するときx=aで極大値を取る。
(B)f(x)がx=aを境界にして減少から増加に変化するときx=aで極小値を取る。
(3)極大,極小と微分係数
f(x)がx=aで微分可能であり、x=aにおいて極値をとるならば
f'(a)=0
曲線の凹凸の判定、変曲点
(1)(A)f''(x)>0となっている区間では、曲線y=f(x)は下に凸(B)f''(x)< 0となっている区間では、曲線y=f(x)は上に凸
(2)変曲点
曲線の凹凸が入れ替わる境になる点を変曲点という。
f(x)が2回微分可能であり、f"(a)=0であるとき、
x=aの前後でF"(x)の符号が変わるならば、曲線-=f(x)上の点(a,f(a))は変曲点となる。
漸近線
曲線y=f(x)が原点から遠ざかるにつれて直線に限りなく近づくとき、その直線を漸近線という。
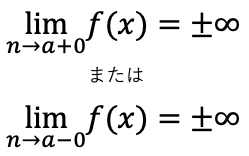 →直線x=aが漸近線
→直線x=aが漸近線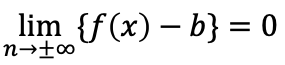 →直線y=bが漸近線
→直線y=bが漸近線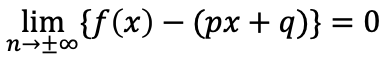 →直線x=px+qが漸近線
→直線x=px+qが漸近線第二次導関数と極大極小
関数f(x)が連続な第二次関数をもつとき。(A)f'(a)=0,f"(a)>0↔︎f(a)は最小値
(B)f'(a)=0,f"(a)< 0↔︎f(a)は最大値
速度,加速度
数直線上を移動する点Pの座標xが時刻tの関数としてx=f(x)で表されているとき(A)点Pの速度は
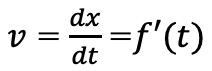
(B)点Pの速さは
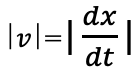
(C)点Pの加速度は
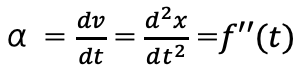
平面上の点の移動
(A)点Pの速度は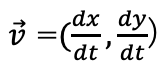
(B)点Pの速さは
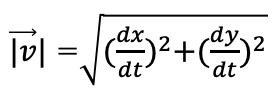
(C)点Pの加速度は
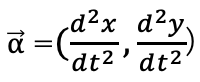
加速度の大きさは
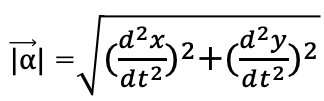
近似値
hが0に近いときf(a+h)≒f(a)+f'(a)hxが0に近いときf(x)≒f(0)+f'(0)x
-----------------------------------------------------