規則性
----------------規則性(目次)-----------------周期算/日暦算
方陣算
----------------------------------
周期算
例題1:以下のように特定の規則によって数が並んでいる。4,6,7,2,4,6,7,2,......
(1)始めから110番目の数はいくつか。
(2)始めから110番目までの和はいくつか。
(1)(4,6,7,2)の4つの数が繰り返し現れている。
この4つが110番目までに何個現れるかを求める。
110÷4=27あまり2
(4,6,7,2),(4,6,7,2)..(4,6,7,2),4,6
(4,6,7,2)は27個ある。
110番目の数は6
(2)110番目までの数の和を求める。
(4,6,7,2)の和が19であり、110÷4=27あまり2より
(4,6,7,2)の塊が19こと4,6が並んでいるので, 19×27+4+6=523
算数塾リンク(オンラインor自宅)↓
算数塾の個別指導
例題2:等差数列
ある規則にしたがって数が並んでいる。
4,7,10,13,...
(1)30番目の数は何ですか?
(2)154は何番目の数は?
(3)1番から30番目の数の和は何ですか?
例題2解答
(1)この数列は隣同士の数の差が3になっている。
はじめの数である 30番目の数は4に3を(30-1=)29個足すので、
4+3×29=91
(2)154に何個3を足されているかを求める。
4+3×(□-1)=154
→3×(□-1)=150
□=51(番目)
(3)(1)より30番目の数は91である。
一番目から30番目までの数「4+7+10+13+....88+91」に
これを反対にした「91+88+...+13+10+7+4」を足すと95が30個できる。
4+7+10+13+....88+91=95×30÷2=1425
日暦算(ひれきざん)
特定の日付けの100日後の日付けを求める問題。2月、4月、6月、9月、11月が31日で無いと記憶していれば解答できる。
ゴロは西向く侍(にしむくさむらい)
侍が11月である。他の4月、6月、9月。11月は30日である。
2月だけは28日しか無い。(うるう年は2月は29日になる。
うるう年は西暦が4で割りきれてかつ100で割り切れない年である。
ただ400で割り切れる年はうるう年である。)
[できる生徒はアドリブで日暦算ができることもある]
6月4日から考えて200日目は何月何日ですか?
解答:
6月4日から数えて200日目は5月の4日+200-1=203(日)
一ヶ月はおおよそ30日であり
30×6=180日だが近い。
6月、7月、8月、9月、10月、11月のうち
6月,9月と11日が30日の月であり、残り3月は31日である。
6月から11月までの日数の合計は30×3+31×3=183(日)
203-183=20日
12月1日から20日を足すと
12月21日_答え
方陣算(ほうじんざん)
例題1:碁石を正方形の形に敷き詰めたら9個あまりました。
そこでたても横も1列ずつ増やそうとしたら、
22個足りませんでした。
碁石は全部で何個ありますか?
解答:
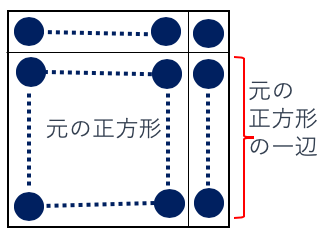
元の正方形の一辺の個数は(あまり+不足-1)÷2
(9+22-1)÷2=15(個)
碁石の数は15×15=225(個)
例題2:碁石を正方形の形に敷き詰めます。
最も外側の個数が44個のとき、碁石は全部で何個ありますか。
解答;
以下の図のように4区間に区切って考えると、正方形の一辺の個数は11個なので。
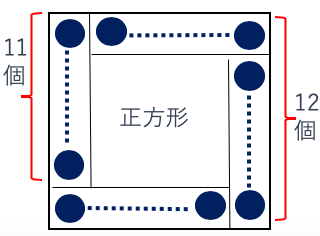
12×12=144(個)
【中学受験用】塾の復習テストで高得点を取るための「復テ対策講座」
----------------規則性(目次)-----------------
周期算/日暦算
方陣算
----------------------------------
Short Notes
Homeに戻る