コメント説明" />
図形の性質
図形の性質分野は中学の幾何的な内容も入り問題のレパートリーが豊富である。
メネラウスなど覚える定理も多彩である。
中学分野も幅広く絡んでくることもあり、この分野だけは5割取れない生徒も多い。
共通テストでは図形の性質は選択分野である。この分野を捨て、整数と確率を選択した方が無難。
-------------------図形の性質_目次------------------
三角形の五心/内角の二等分線の定理
外角の二等分線の定理/メネラウスの定理
チェバの定理/方べきの定理
方べき証明/接弦定理
トレミーの定理
--------------------------------------
三角形の五心
内心:角の二等分線の交点(内接円の中心)
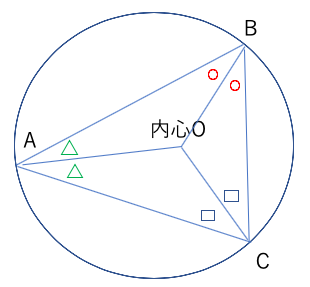
外心:3辺の垂直二等分線の交点(外接円の中心)
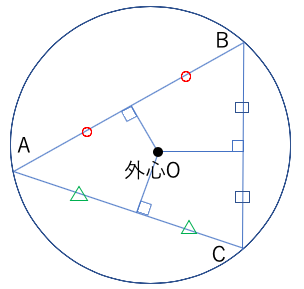
重心:中線の交点(中線は2:1で内分される)
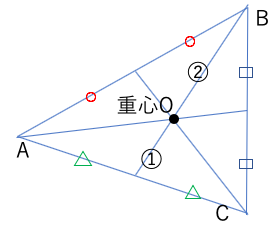
[垂心:垂線の交点]
[傍心:内角の二等分線と2つの外角の二等分線の交点]


内角の二等分線の定理
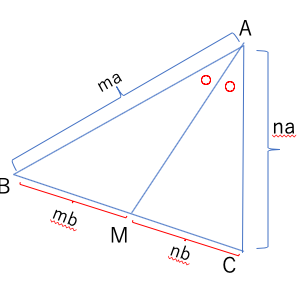
AB:AC=BM:MC
内角の二等分線証明
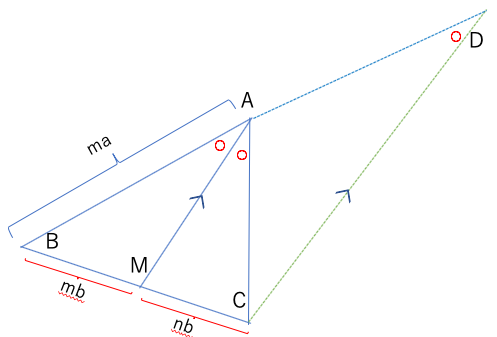
線分MAと並行な直線CDを引く。
BAの延長とCDの交点をDとする。
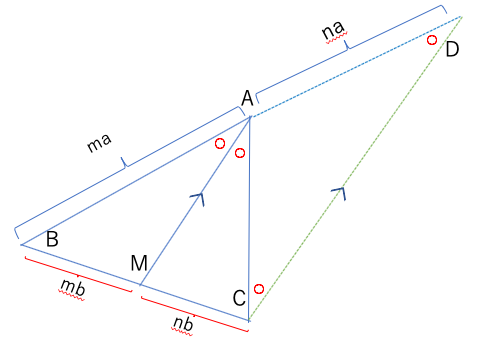
三角形BMAと三角形BCDが相似
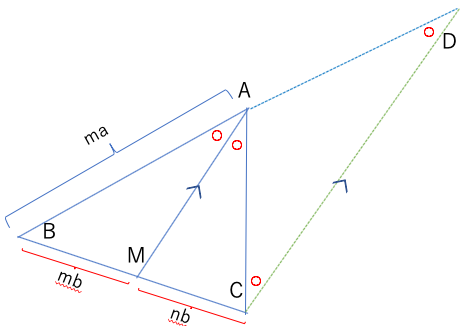
線分AM//線分DCより
角BAM=角BDC(同位角)
角MAC=角ACD(錯角)
→角ADC=角ACD
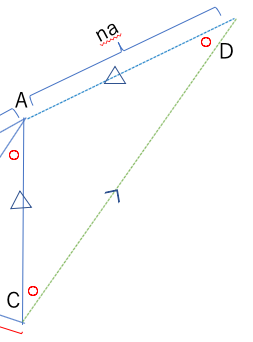
角ADC=角ACDより三角形ACDはAC=ADの二等辺三角形
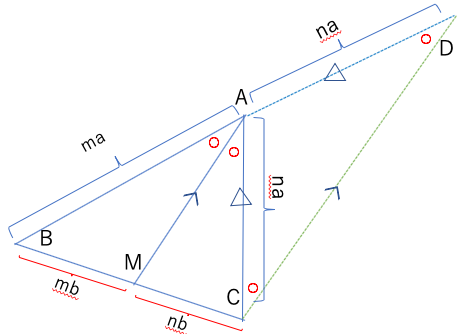
AB:AC=BM:MC
外角の二等分線の定理
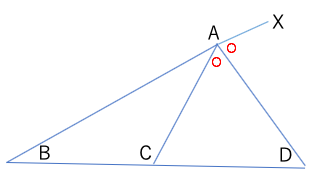
角CABの外角の二等分線と直線BCの延長との交点を点Dとすると、
AB:AC=BD:CD
が成り立つ。
外角の二等分線の定理の証明
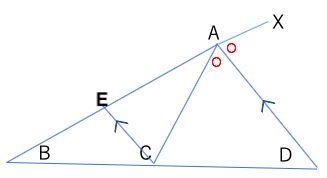
点Cを通り、ADに並行な補助線を引くと
三角形ABDと三角形EBCが相似となり、
AB:EA=BD:CD...①となる。
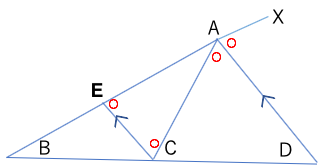
角XAD=角AEC(同位角)
角DAC=角ACE(錯角)
三角形AECはAE=ACの二等辺三角形
①より
AB:AC=BD:CD
メネラウスの定理
下図の三角形において、・・=1
が成り立つ。
図の中に狐の図形を発見したらメネラウスを使用できる。
頂点A→分点→頂点B→分点→頂点C→分点→頂点Aのように
頂点間で分点を経由しながら一周する旅をする。
旅は右向きでも左向きでも構わない。
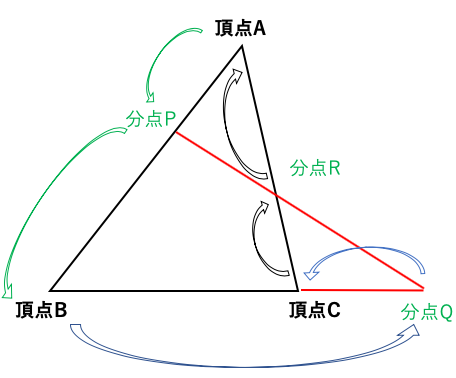
三辺の延長上の外分点が1個か3個の場合にはメネラウスの定理を使い、
0個か2個の場合はチェバの定理を適用する。
チェバの定理
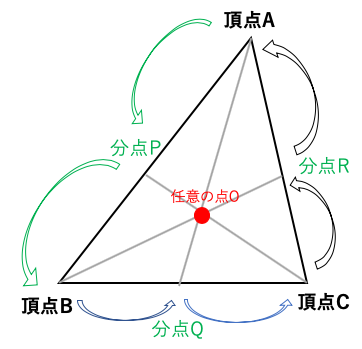
下図の三角形において、・・=1
が成り立つ。
任意の点Oを取り、頂点とOに直線を引き、三角形との交点を分点とする。
メネラウスと同様に、
頂点A→分点→頂点B→分点→頂点C→分点→頂点Aのように
頂点間で分点を経由しながら一周する旅をする。
旅は右向きでも左向きでも構わない。
方べきの定理
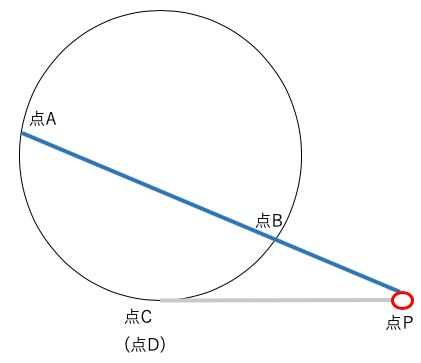
PA・PB=PC・PD
方べきの定理は相似形ができることを利用している。
図1↓
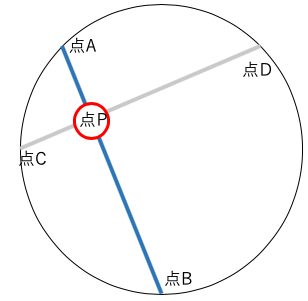
図2↓
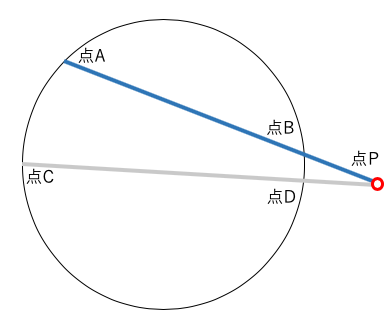
PA・PB=PC2
図3↓


方べきの定理証明
対頂角より、角BPD=角APC
ADを弦とする円周角により
角DBP=角ACP
図1↓
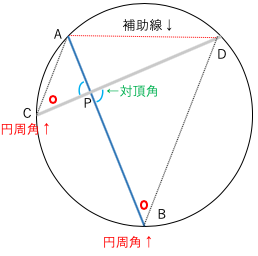
対頂角より、角BPD=角APC
ADを弦とする円周角により
角DBP=角ACP
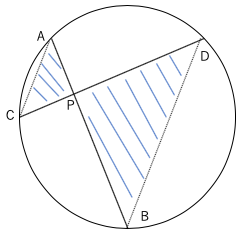
三角形DBPと三角形PACは相似である。(二角相等)
PD:PB=PC:PAよりPD・PA=PB・PC
[ここで証明は終わりだが、以下にPD:PB=PC:PA→PD・PA=PB・PCも証明しておく]
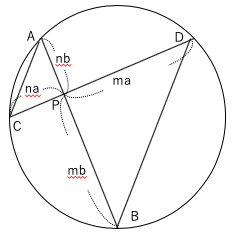
三角形DBPと三角形PACの相似比をm:nとし、
PD:PB=PC:PA=a:b
とするとPA,PBとPA,PCは上図のように表せる。
PD・PA=ma・nb=mnab
PB・PC=mb・na=mnab
PD・PA=PB・PC
図2↓
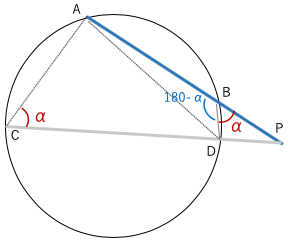
図2において、円周角ACD(α度)の逆側の円周角DBAは180度-α
角PBD=180-(180-α)
=α
三角形PBDと三角形PCAは相似(二角相等)
図1と同様に定理が成り立つ。
図3↓
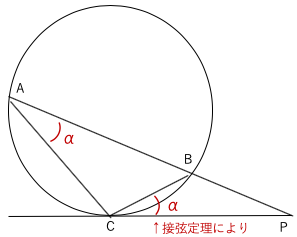
図3において、弦BCにおける接弦定理において
角BAC=角PCB
三角形PACと三角形PCBは相似(二角相等)
図1と同様に定理が成り立つ。
接弦定理
接線と弦のなす角=弦に対する円周角
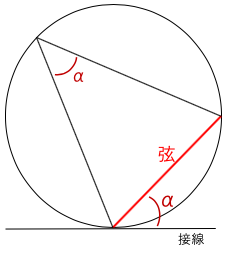
接弦定理の証明は円周角αを中心を通るように動かすと以下の図のように証明できる。
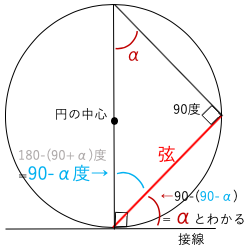

この分野は定理をうろ覚えの受験生も多く注意したい。


トレミーの定理
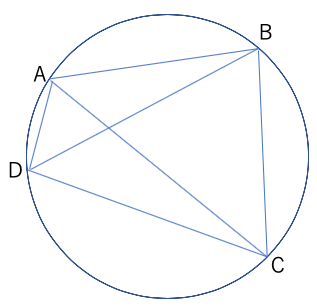
円に内接する四角形ABCDにつき、
AC×BD=AD×BC+AB×DC
が成り立つ。
角ABDと同じ角CBXとなる点Xを線分AC上に置く。
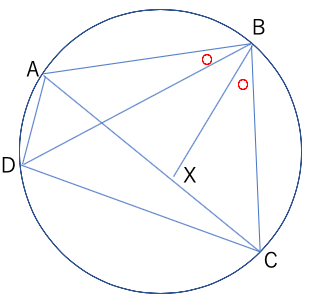
三角形ABDと三角形DBCは相似(二角相当[角ABX=角DBC(○+角DBX),角BAX=角BDC(△)])
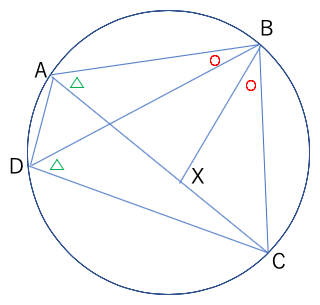
AX:DC=AB:DB
AX×DB=DC×AB...(1)
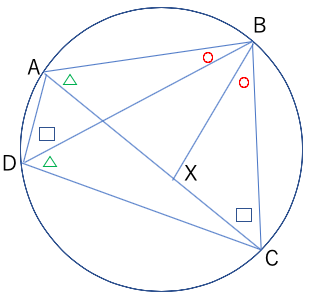
三角形ADBと三角形XCBは相似(二角相当[角ABD=角XBC(○),角ADB=角ACB(□)])
AD:XC=DB:CB
AD×CB=XC×DB
XC×DB=AD×CB...(2)
(1)+(2)より
DB×(AX+XC)=DC×AB+AD×CB
DB×AC=AB×DC+AD×BC
-------------------図形の性質_目次------------------
三角形の五心/内角の二等分線の定理
外角の二等分線の定理/メネラウスの定理
チェバの定理/方べきの定理
方べき証明/接弦定理
トレミーの定理
--------------------------------------































