旅人算/ 流水算
流水算(応用編)/ 通過算
時計算/ 歩数と歩幅
-------------------------------------------
旅人算
速さの違う二人が同じ道を移動しており、追い越したり、出会う時の時間を考える問題。Aの歩く速さを分速100m、Bの歩く速さを分速50mとする。
AとBは同じ方向に歩いており、AはBの後方300mからBを追いかけるとする。
(追いつくまでの時間)=(二人の最初の距離)÷(速さの差)
ここでは(追いつくまでの時間)=300÷(100-50)
(追いつくまでの時間)=6(分)
二人が離れた場所から向かい合って進むとき、距離は750mとする。
(出会うまでの時間)=(二人の距離)÷(速さの和)
(出会うまでの時間)=750÷(100+50)
=5(分)
流水算
流れる川を二つの船が上りまたは下りで移動する際の速さやかかる時間を算出する特殊算船が上りの場合には川の流速を引いたものを速さとする。
船が下りの場合には川の流速を足したものを速さとする。
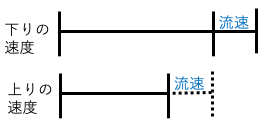
速さを求める
例題:下りが時速20km、上りが時速5km、川の流れの速さと静水時の船の速さを求めなさい。解答:
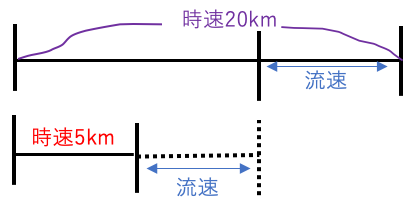
(流れの速さ)=(下りの速さ-上りの速さ)÷2
(流れの速さ)=(20-5)÷2=7.5[km/h]
(静水時の船の速さ)=(上りの速さ+下りの速さ)÷2
(静水時の船の速さ)=(20+5)÷2=12.5[km/h]
[別解]
(静水時の船の速さ)+(流れの速さ)=20...①
(静水時の船の速さ)-(流れの速さ)=5...②
①+②より
2×(静水時の速さ)=25
(静水時の速さ)=12.5(km/h)
【中学受験用】塾の復習テストで高得点を取るための「復テ対策講座」
流水算(応用編)
船が移動する距離が同じ場合、船の速さの比とかかる時間の比が逆比になっていることを利用する。
船の下りと上りの速さの比3:1→下りと上り移動時間の比1:3
例題:下流のA地点、上流にB地点があります。
船がA(下流)からB(上流)まで35分で上り、
BからAに14分で下りました。
川の流速は分速6mとし、AB間の距離を求めなさい。
時間の比が35:14=5:2なので、
速さの比は逆比の2:5
上りの速さを2x,下りの速さを5xとすると 上り)2x=静水時の速さ-6...①
下り)5x=静水時の速さ+6...②
静水時の速さは3.5x
上りの速さが2xなので
流速は3.5x-2x=1.5x
1.5x=6よりx=4
上りの速さ=2x=8(m/分)
[下りの速さ=5x=20(m/分)]
(AB間の距離)=(上りの速さ)×35(分)
=8×35
=280(m)
通過算
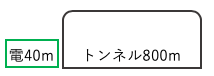
トンネルに入り始めてから出るまでは{(トンネルの長さ)+(電車の長さ)}÷電車の速さトンネル:800m,電車40m,電車の速さ:秒速20m
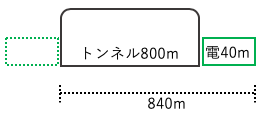
ここではトンネルに入り始めてから出るまでの時間を求めると
(800+40)÷20=42(秒)
時計算
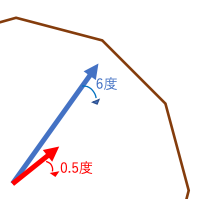
時計の長針は1分間に6度進む。短針は1分間に0.5度進む。
長針と短針の距離は1分間に5.5度近づく
(追い越した後は5.5度遠ざかる。)
時計算:例題
1時と2時の間で長針と短針の角度の差が8度になるのは何時何分か?
時計算:例題解答
1時の時点で長針と短針の角度は360÷12=30(度)
30度の角度の差が0度になるまでにかかる時間は
(30-8)÷5.5=4(分)
答え1時4分
歩数と歩幅
歩数算:例題1A氏が3歩で歩く距離とB氏が5歩で歩く距離が等しい時
AとBの歩幅の比を求めよ。
歩数算:例題1答え
AとBの歩幅の比はAとBの歩数の比の逆比5:3になる。
小学生をやる気にさせる!具体的な方法
-----------------------
-------------------------------------------
旅人算/ 流水算
流水算(応用編)/ 通過算
時計算/ 歩数と歩幅
-------------------------------------------
Short Notes
Homeに戻る