Short Notes

三角関数

加法定理などの公式が冗長でかなり覚えにくい。
河合偏差値４０程度の生徒は加法定理がうろ覚えで三角関数の合成に苦労する。
下位、中位の生徒にとってはきつい分野。
加法定理や和積の公式は導出に手間がかかり、暗記が煩雑なため語呂で覚えてしまった方が良い。

sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α±β)=cosαcosβ∓sinαsinβ
cos(α±β)=cosαcosβ∓sinαsinβ
tan(α±β)=

\frac{tanα±tanβ}{1∓tanαtanβ}

例題：２直線y=2x+1とy=

\frac{1}{3}

のなす角θを求めよ。

解答：y=2x+1とy=

\frac{1}{3}

のなす角をそれぞれθ₁,θ₂とすると。

tanθ₁=

\frac{1}{3}

,
tanθ₂=2

θ＝θ₁-θ₂

tanθ

=tan(θ1-θ2)

=

\frac{tanθ1-tanθ2}{1+tanθ1×tanθ2}

=(2-

\frac{1}{3}

)÷(1+2×

\frac{1}{3}

)

=1(答え)

sin2α=2sinαcosα
ゴロ：サインは錦織にしこり cos2α=cos2α−sin2α
=2cos2α−1(ニコス[card]に１万引かれる)
=1−2sin2α
tan2α=

\frac{2tanα}{1−tan2α}

sinはすぐ加法定理で導出できるが、cosとtanは暗記した方が速い。

sin²

\frac{α}{2}

\frac{1-cosα}{2}

cos²

\frac{α}{2}

\frac{1+cosα}{2}

tan²

\frac{α}{2}

\frac{1-cosα}{1+cosα}

三倍角の公式は共通テストでの時間省略になるが、
加法定理、二倍角を使った公式導出に時間がかかるため暗記した方が楽。
sin3θ=3sinθ-4sin³θ
ゴロ：サンシャイン引いて夜風が身に染みる。

cos3θ=4cos³θ-3cosθ
ゴロ：良い子のみんなで引っ張る神輿(みこし)

asinθ+bcosθ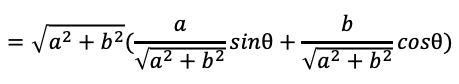

\sqrt{a^{2} + b^{2}}

(sinθcosα+cosθsinα)
=

\sqrt{a^{2} + b^{2}}

sin(θ+α)
１行目から２行目の変形は以下のような直角三角形を強引に作り出しsinαとcosαに変換している。

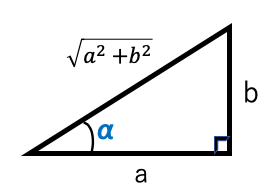
２行目から３行目はsin(a+b)の加法定理を利用している。

積和の公式は少し時間をかければ加法定理での導出も可能だが、
和積の公式はゴロで暗記した方が共通テストなどで時間が省略でき、有利になる。

cosA+cosB=2cos

\frac{A+B}{2}

cos

\frac{A-B}{2}

cosA−cosB=−2sin

\frac{A+B}{2}

sin

\frac{A-B}{2}

sinA+sinB=2sin

\frac{A+B}{2}

cos

\frac{A-B}{2}

sinA−sinB=2cos

\frac{A+B}{2}

sin

\frac{A-B}{2}

↑５回聞けば大体覚えられるが周期的に聞いてないと忘れる。
積和の公式は簡単なので導出しても良い。
「試験合格プロジェクトを成功させる方法」

↓積和の公式。
sinαcosβ=

\frac{1}{2}

(sin(α+β)+sin(α−β))
cosαsinβ=

\frac{1}{2}

(sin(α+β)−sin(α−β))
cosαcosβ=

\frac{1}{2}

(cos(α+β)+cos(α−β))
sinαsinβ=−

\frac{1}{2}

(cos(α+β)−cos(α−β))

例題１：sin40°×sin80°×sin160°を計算せよ。
sin200°＝-0.342とする。

例題２：cos20°+cos70°+

\sqrt{2}

cos155°
を計算せよ。

リンク

例題１解答：まずsin40°×sin80°に積和の公式を適用する。
与式＝-

\frac{1}{2}

\frac{1}{4}

\frac{1}{4}

= $\frac{1}{4}$
[-sin160°=sin200°を用いた]
=
例題２解答：
2cos $\frac{20+70}{2}$ cos $\frac{20-70}{2}$

=

Short Notes
Homeに戻る