関数と極限(数３)
分数関数
k > 0 のとき↓
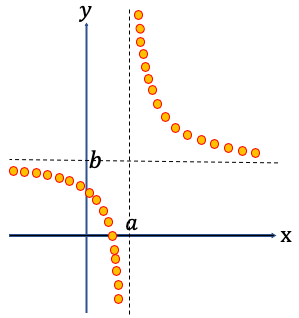
k < 0 のとき↓
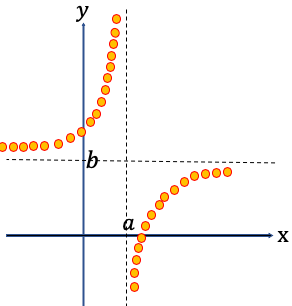
無理関数
y=のグラフ↓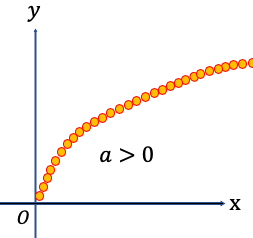
y=のグラフ↓
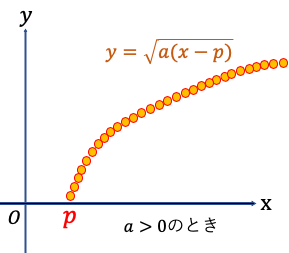
y=のグラフがx軸方向にpだけ右に移動する。
逆関数
y=f(x)をxの方程式だと考え、x=g(y)
xとyを入れ替えて得られる関数y=g(x)をy=f(x)の逆関数をいいy=f-1(x)で表す。
合成関数
g(x)＝x+3f(x)=x2
合成関数f(g(x))=(x+3)2
g○f=g(f(x))と表す。
[右側の関数からxを代入する。f→gの順序]
f○g≠g○f
収束と発散
極限の公式
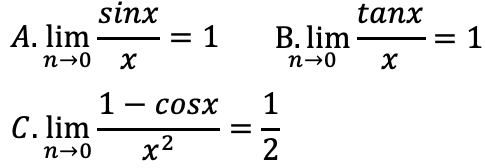
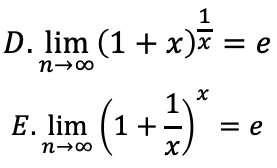
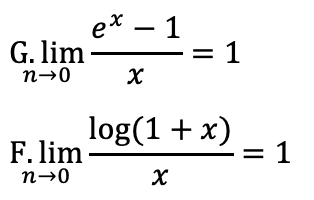
数列の極限
(I)数列{nk}の極限k：正の定数
無限数列において、nが無限に大きくなるにしたがって、
anが一定の値αに近づいていくとき、
数列{an}はαに収束するといい、
αを数列{an}の極限値という
数列の極限値がαである場合には以下のように書く
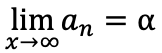
数列{an}が収束しないとき、
{an}は発散するとする。
(一)nを無限に大きくすると、anが無限に大きくなるとき
数列{an}は正の無限大に発散すると定義し、以下のように記載する。
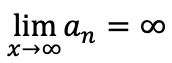
(二)nを無限に大きくすると、 anが負でその絶対値|an|が無限に大きくなりさいに、
数列{an}は負の無限大に発散するといい、
以下のように記載する。
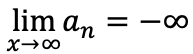
(三)
数列が収束も発散もしないとき
正の無限大にも負の無限大にも発散しないとき数列は振動するという。
無限等比数列の極限
無限等比数列の収束,発散
(A)数列{rn}の極限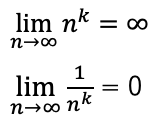
(B)無限等比数列{rn}が収束する⇔-1 < r ≦ 1
無限級数の収束,発散
(A)無限級数{an}において、a1+a2+...+an+...
の式を無限級数と定義し、以下のように記載する。
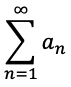
anを無限級数の第n項とする。
(B)無限級数の収束・発散
(C)無限級数の和に関する性質
無限級数
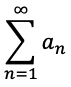
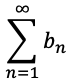
が収束し、
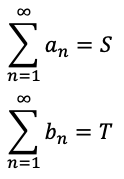
であるとき,
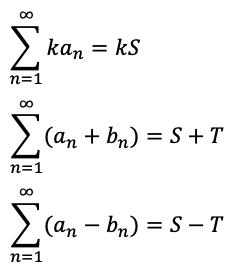
(D)無限級数と無限数列
(α)無限級数
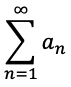が収束するとき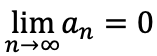
(β)数列{an}が0に収束しない場合、無限級数
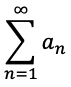は発散する。無限等比級数の収束,発散
(一)初項a,公比rの無限等比数列から無限級数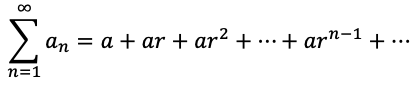
を初項a、公比rの無限等比級数という。
（二）無限等比級数の収束、発散
(A)a=0のとき
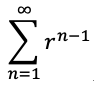は収束しその和は0(B)a≠0のとき|r|< 1ならば
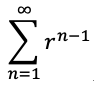は収束し、その和は|r|> 1ならば
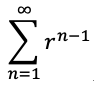は発散する。関数の極限値と四則
数列{an},{bn}が収束して、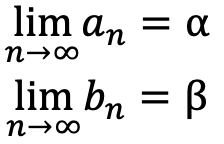
のとき
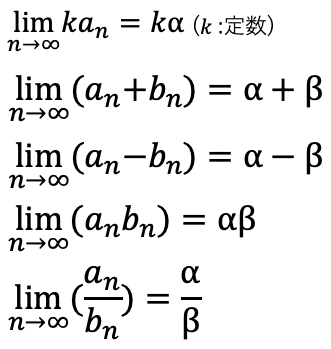
ただしβ≠0
関数の極限値と大小関係
(一)数列{an},{bn}において、
an≦bn(n=1,2,..)のとき
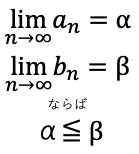
(二)
数列{an},{bn}において、
数列an≦bnのとき
→
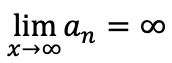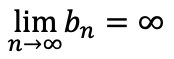
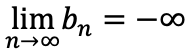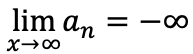
→(三)はさみうちの原理
数列{an},{bn},{cn}について、
an≦bn≦cn(n=1,2,..)のとき
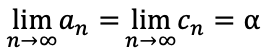
のとき{bn}は収束し
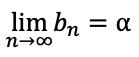
関数の連続
関数の連続とは関数がつながってることである。証明が大変なので以下のように証明する必要がある。
aを関数f(x)の定義域に属する値とするとき、
関数f(x)がx=aで連続であることと
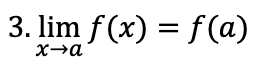
が成立することは同義である。
つまり確認として以下の３点が必要である。
1.
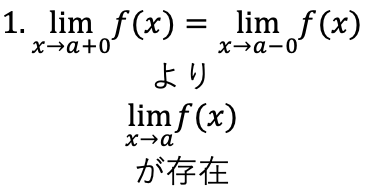
(1.右側極限と左側極限が等しい)
2.f(a)が定義されている。
3.
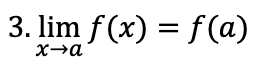
中間値の定理
a≦x≦bで連続な関数f(x)を考える。f(a)とf(b)の間にある任意の実数kに関して、
f(c)=kとなるc(a≦x≦b)が存在する。
-----------------------------------------------------