二次関数
中学のxy座標平面の概念を分かっていれば、習得も応用問題も容易な分野だがなぜかここで躓く生徒が多い。xの変域での場合分けなどが少し煩雑なだけの楽な分野。
ぜひ得点源にしたい。ただ中学の方程式が分からずにつまづく下位層生徒が多い。
頂点(p,q)で傾きがaの二次関数の式
y=a(x-p)2+q
pの値が１増える(=xから引く数が増える)とグラフはx軸方向に１移動する。
qの値が増えるとグラフはy軸の正の方向に１移動する。
aの値が増えるとグラフは狭まり、減ると広まる。
a>0の場合グラフは下に凸、a< 0の場合グラフは上に凸
【東京大学法学部受験突破の勉強法】 不器用だからできる“逆転合格の極意”
平方完成
y=ax2+bx+cのグラフをy＝α(x-p)2+qの形に直してグラフの頂点をわかりやすくする操作。(x+y)2=x2+2xy+y2の公式を利用する。
例：y=x2+10xのグラフがあった場合
10xを２で割って2×5xとする。
x2+2×5xは
(x+5)2の展開式x2+2×5x+52と二項目まで一致する。
x2+2×5x＝(x+5)2-52と平方完成できる。
最大値、最小値
放物線の軸と範囲によって場合分けを行う。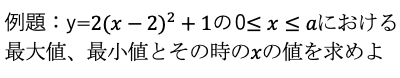
----------------------------------------------------
0≤a<2のとき
x=0の時に最大値f(0)=9をとり、
x＝aの時に最小値f(a)をとる。
----------------------------------------------------
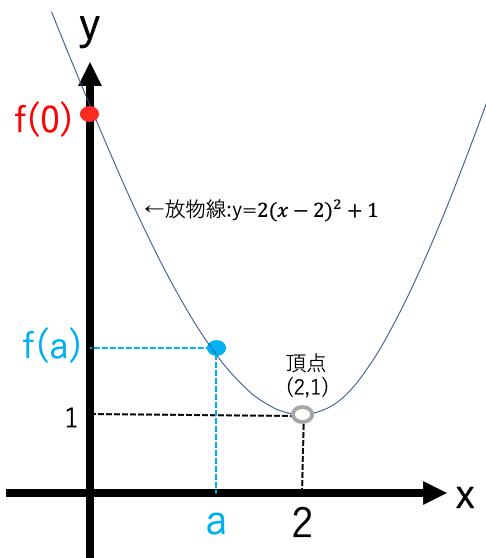
2≤a<4のとき
x=0の時に最大値f(0)=9をとり、
x＝2の時に最小値1をとる。
----------------------------------------------------
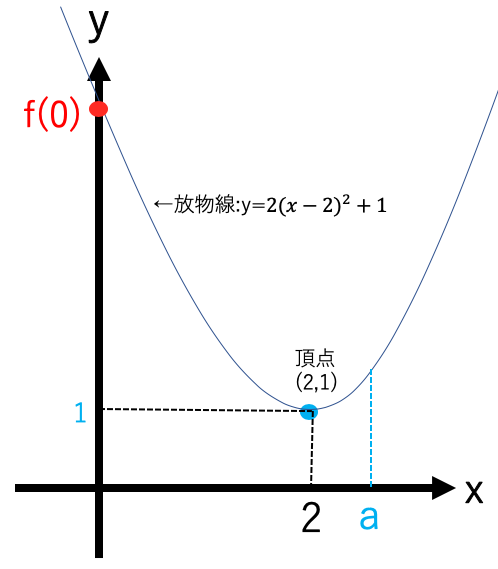
a=4のとき
x=0、x＝4の時に最大値f(0)=f(4)=9をとり、
x＝2の時に最小値1をとる。
----------------------------------------------------
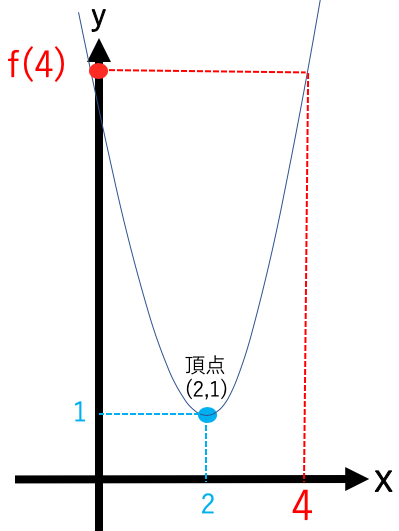
4<aのとき
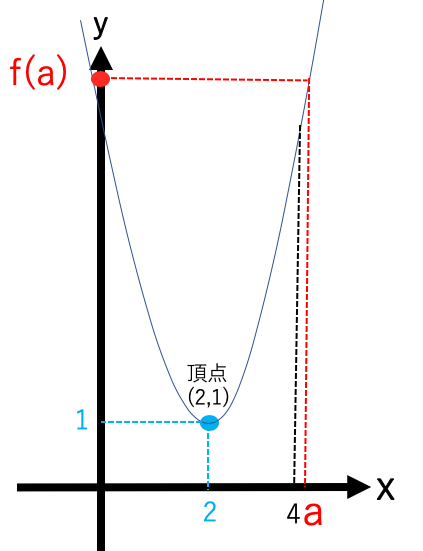
x＝4の時に最大値f(a)をとり、
x＝2の時に最小値1をとる。
----------------------------------------------------
二次関数の対称移動
x軸について対称移動：yを-yに変えるy軸について対称移動：xを-xに変える
原点について対称移動：xを-xに,yを-yに変える
例：二次関数
y=x2-4x+9[備考：原点(2,5)]
をx軸について対称移動
-y=x2-4x+9
-----------------------
y=x2-4x+9
をy軸について対称移動
y=(-x)2-4(-x)+9
--------------------------
y=x2-4x+9
を原点について対称移動
-y=(-x)2-4(-x)+9
Short Notes
Homeに戻る