図形と方程式
数学２の図形は点と直線の距離の公式を多用するなど公式、パターンの力で回答できる場合も多く、数学Aの図形の性質や中学図形程センスは要求されない。
二点間の距離
二点A(x1,y1),B(x2,y2)の距離は
(二点間の距離)2=(x1-x2)2+(y1-y2)2
大学教員視点だからどんな難関大学でも使える！志望理由書で最も大事な考え方テキスト（スマホ対応
内分と外分
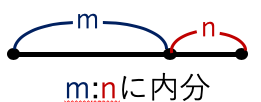
点A(x1,y1),点B(x2,y2)とし、
線分ABをm:n に内分する点Pは
内分点P=
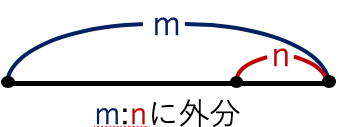
線分ABをm:nに外分する点Qは
外分点Q=
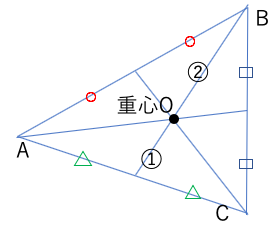
三角形の重心
重心：三角形の中線３本の交点。(数学の重心と物理での力学的重心は一致する)3点(x1,y1)(x2,y2)(x3,y3)を頂点とする△ABCの重心Gの座標は
G=( )
直線の方程式
２直線y=a1x+b1とy=a2x+b2において２直線が直交する場合a1×a2=-1
並行の場合a1＝a2
点と直線の距離
点(x0,y0)と直線ax+by+c=0の距離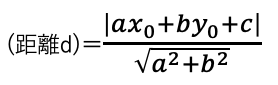
円の方程式
原点が中心である円x2+y2=r2
中心の座標が(a,b)である円
(x-a)2+(y-b)2=r2
軌跡と領域
例題１：２点A(1,2),B(5,6)について、AP:PB=2:1を満たす点Pの軌跡を求めよ。点Pの座標をP(x,y)とおくと
AP:PB=2:1より
2AP=1PB
4AP2=PB2
(1-x)2+(2-y)2=(x-5)2+(y-6)2
8x+8y-56=0
→x+y-7=0
(求める軌跡は直線y=-x+7)
軌跡と領域はかなり難しい分野。
点と直線の距離を多用しがち。
不等式の表す領域
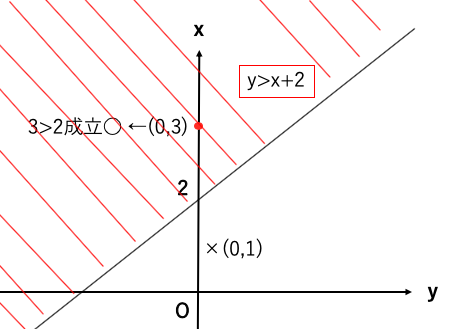
例題：y>x+2の領域を図示せよ。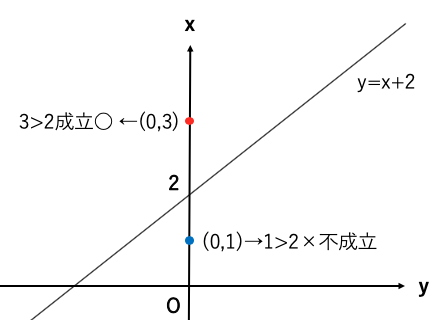
どちらが正領域、負領域かわからない場合は領域内の計算しやすい座標を等式(例y=x+2)代入して
正領域、負領域を判定する。
Short Notes
Homeに戻る